Question

The pressure caused by the gravitational pull inside the earth at a distance a measure from its centre, when its mass and radius are m and R respectively is given by
A.$\dfrac {8}{3} \dfrac {G{m}^{2}}{\pi {R}^{4}}(1+ \dfrac {{a}^{2}}{{R}^{2}})$
B.$\dfrac {8}{3} \dfrac {G{m}^{2}}{\pi {R}^{2}}(1- \dfrac {{a}^{2}}{{R}^{2}})$
C.$\dfrac {3}{8} \dfrac {G{m}^{2}}{\pi {R}^{4}}(1-{( \dfrac {a}{R})}^{2})$
D.$\dfrac {8}{3} \dfrac {G{m}^{2}}{\pi {R}^{4}}(1- \dfrac {a}{R}$

Answer 1

To solve this problem, use the equation for pressure which is opposing the force exerted by the earth's surface. Find the volume of earth. Thus, find the density of the earth. Then, use the expression for internal gravity of earth. Substitute the value of internal gravity and density of earth in the equation for pressure opposing the force. Then, integrate this equation. Thus, the obtained expression will be the pressure caused by the gravitational pull inside the earth.

Complete answer:

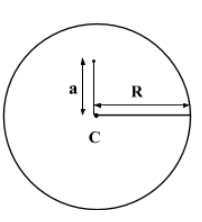
Pressure opposing the force is given by,
$dp = \rho {g}_{r} dr$ ...(1)
Where,${g}_{r}$ is the earth's internal gravity
$r$ is the distance from earth's center
$\rho$ is the density of earth
We know, density of earth is given by,
$\rho= \dfrac {m}{V}$ ...(2)
Volume of earth is given by,
$V= \dfrac {4}{3} \pi {R}^{3}$
Substituting this value in the equation. (2) we get,
$\rho= \dfrac {m}{ \dfrac {4}{3} \pi {R}^{3}}$ ...(3)
Earth's internal gravity is given by,
$\Rightarrow {g}_{r}= \dfrac {GMm}{{R}^{3}}$ ...(4)
Substituting equation. (3) and (4) in equation. (1) we get,
$\Rightarrow dp = \dfrac {m}{ \dfrac {4}{3} \pi {R}^{3}}. \dfrac {GMm}{{R}^{3}} dr$
$\Rightarrow dp= \dfrac {3G{m}^{2}r}{4 \pi {R}^{6}} dr$
Integrating above equation we get,
$p= \dfrac {3G{m}^{2}}{4 \pi {R}^{6}} \int_{a}^{R} rdr$
$\Rightarrow p = \dfrac {3G{m}^{2}}{4 \pi {R}^{6}} \dfrac {1}{2} ({R}^{2} –{a}^{2})$
$\Rightarrow p = \dfrac {3G{m}^{2}}{8 \pi {R}^{4}} (1-{( \dfrac {a}{R})}^{2})$
Hence, the pressure caused by the gravitational pull inside the earth is $\dfrac {3}{8} \dfrac {G{m}^{2}}{\pi {R}^{4}}(1-{( \dfrac {a}{R})}^{2})$.

So, the correct answer is option C i.e. $\dfrac {3}{8} \dfrac {G{m}^{2}}{\pi {R}^{4}}(1-{( \dfrac {a}{R})}^{2})$.

Note:
At the center of earth or any other planet, the gravitational pressure can be balanced by outward thermal pressure due to the fusion reactions occurring every time. Due to this thermal pressure, the effect of gravitational pressure gets temporarily halted. At the center, gravitational pressure can produce heat as well. Near the center of earth where gravity is nearly zero, pressure increases more slowly. While near the surface, where gravity is more as compared to the center, pressure increases uniformly.