Question
Question: The power factor of the LCR circuit at resonance is:...
The power factor of the LCR circuit at resonance is:
Solution
First define the power in LCR circuit which is given by:
Pqv=erms×irms.cosϕ
The term cosϕ is the power factor. Then apply the condition of resonance where capacitance gets equal to inductance. Then calculate the value of ϕ i.e, phase difference between the voltage and current and then analyze the expression of the angle ϕ.
Complete step by step solution:
First, let us see what the power factor of LCR is. So, let us see the circuit of LCR.
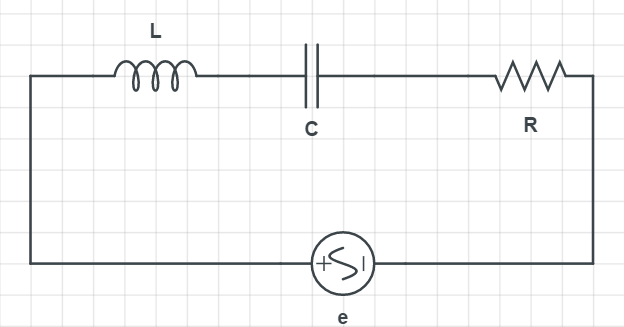
Let e=e0sinωt be the alternating voltage applied across the series combination of the pure inductor, capacitor and resistor and let ϕ be the phase difference between the applied e.m.f or voltage and current.
Therefore, the average power is given by:
Pw=erms×irmscosϕ......(i)
The factor is given in the equation (i), cosϕ is called the power factor.
At resonance, when the frequency of the voltage is adjusted so that at a particular frequency, XL=XC then Z = R. Basically at resonance, inductive impedance is equal to the capacitive impedance of the circuit.
We know that the power factor is the ratio of true power to the apparent power consumed in the circuit and can be written as,
cosϕ=ZR
At resonance, R = Z. Therefore,
cosϕ=1
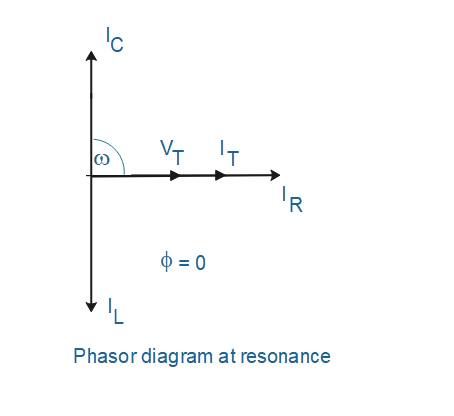
⇒ϕ=0
The above equation implies that voltage across the inductor and capacitor cancels each other. It also implies that the total impedance calculated for the circuit is only due to the resistor. It shows that the phase angle between the current and the voltage is zero. If, ϕ=0 then the power factor is unity.
Note: If ϕ=90∘ i.e. the phase difference between the voltage and the current is 90∘ then the circuit is purely inductive and capacitive. The quantity in equation (i), erms.irms is calculated as true power. At resonance, the power dissipation in the circuit is due to resistance only.
