Question
Question: The potential energy of a particle varies according to the graph shown. Force acting on it varies ac...
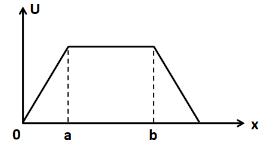
The potential energy of a particle varies according to the graph shown. Force acting on it varies according to which of the following graphs:-
(A) 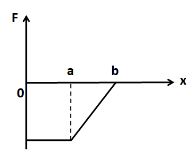
(B) 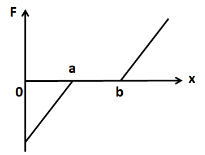
(C) 
(D) 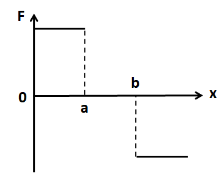
Solution
To solve this question, we have to deduce a relation between the potential energy and the conservative force. For this, we need to consider the work done by a conservative force on a particle, and relate it with the change in its potential energy.
Complete step-by-step solution
We know that the work done by a force on a particle is equal to the product of the force and the displacement. If a force of F acts on a particle to displace it through a small distance dx , then the small work done by this force is given by
dW=Fdx ...............(1)
Let us suppose that this force is a conservative force. This means that this force will have a corresponding potential field, which in turn means that the particle in the potential field will have a potential energy at each point. We know that the change in potential energy of a particle due to a conservative force is equal to the negative of the work done by the force on the particle, that is,
dU=−dW ...............(2)
Putting (1) in (2) we get
dU=−Fdx
Dividing both sides of the above equation by dx , we get
dxdU=−F
Or
F=−dxdU ...............(3)
So the magnitude of the conservative force is equal to the negative of the derivative of the potential energy with respect to the displacement.
From the given graph, there are three intervals of x ; (0,a) , (a,b) , and (b,∞) .
In the interval (0,a) :
We can see that the slope of the graph is constant and is positive in this interval. Let it be equal to m . So we have
dxdU=m
Putting this in (3) we get
F=−m
So the force in this interval is constant and is negative. So it must be represented by a vertical line below the x axis.
In the interval (a,b) :
We can see that the graph is a horizontal line in this interval. This means that the slope is equal to zero. So we have
dxdU=0
Putting this in (3) we get
F=0
So the force in this interval is equal to zero.
In the interval (b,∞) :
We can see that the slope of the graph is constant and is negative in this interval. Let it be equal to −k . So we have
dxdU=−k
Putting this in (3) we get
F=k
So the force in this interval is constant and is positive. So it must be represented by a vertical line above the x axis.
Thus, we obtain the following graph of the force
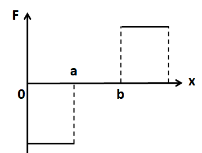
Hence, the correct answer is option C.
Note
We should not forget the negative sign in the relation between the work done by a conservative force and the change in potential energy. We can also confirm this by taking a simple example of a stone falling vertically downwards. Since the gravitational force acts downwards, so the work done by the gravitational force will be positive. Also, since the height of the stone above the ground is decreasing as it falls, so the potential energy of the stone will decrease. This means that the change in potential energy of the stone is negative, when the work done by the conservative gravitational force is positive.
