Question

The potential drop across the 3 Ω resistor is:

A. 1V
B. 1.5V
C. 2V
D. 3V

Answer 1

We are provided with a circuit which has resistances and voltage connected to it as an electrical component. 3Ω and 6Ω are in parallel so apply parallel combination, to find equivalent parallel resistance. This resistance will be in series with $4\Omega$ so apply a series combination. Using the value of the voltage calculate the total current. We know that in parallel connection, voltages across branches are always the same. Hence calculate potential drop across against 3Ω Kirchhoff’s second law.

Complete answer:
We are provided with a circuit which is given as follow.

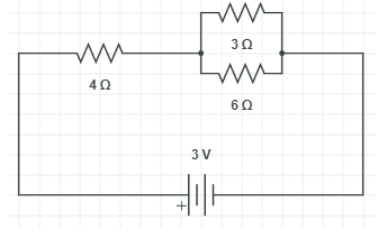
Now we need to find the potential drop across the 3.ohm resistor. The electrical components (resistors) are connected in parallel. So the same voltage appears to each electric component. We know that, in case of parallel circuits, the voltage across each of the components is the same, and the total current flowing through each of the components is the sum of the currents. To find the total resistance or equivalent resistance of all electrical components, the reciprocals of the resistance of each electrical component is added and the reciprocal of sum is taken. Hence, the equivalent resistance will always be lesser than the value of the smallest resistance i.e.,
$\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+......+\dfrac{1}{{{R}_{n}}}$
In this case, 3ohms and 6ohms resistances at the right side of the circuit (shown in circuit) are connected in parallel. Therefore their combined resistance is given as,
$\dfrac{1}{3}+\dfrac{1}{6}=\dfrac{1}{0.5}=2 ohms$
Now the circuit looks like:

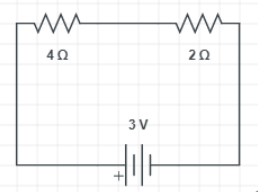
So 4ohms and 2ohms are connected in the series. Therefore the equivalent resistance is 4+2=6 ohms. Let I be the current flowing through circuit the total current in the circuit is given as,
$I=\dfrac{V}{R}=\dfrac{3}{6}=0.5A$
As we already discussed that in a parallel connection, the voltage remains the same across all the components. Therefore, potential drop against the resistances 3Ω is given as
$\begin{aligned} & V=IR \\\ & V=0.5\times 2 \\\ & V=1volts \\\ \end{aligned}$
Hence, the potential drop across the 3Ω resistance is 1 volt .

Therefore option A is correct.

Note:
Electrical components are connected in series and are always connected along a single path, so the same current flow through all the electrical components i.e. resistance (in this case) means, the current through each of the components is same and the voltage against the circuit is the sum of the voltage against each of the components. In the series every device must function for the circuit to be complete. A circuit which is composed solely of the electrical components connected in the series is known as the series circuit. The equivalent resistance of the resistors in series is the sum of the individual. Resistance which is represented as ${{R}_{eq}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}+.......+{{R}_{n}}$.