Question
Question: The potential difference (in V) between points A and B shown in figure....
The potential difference (in V) between points A and B shown in figure.
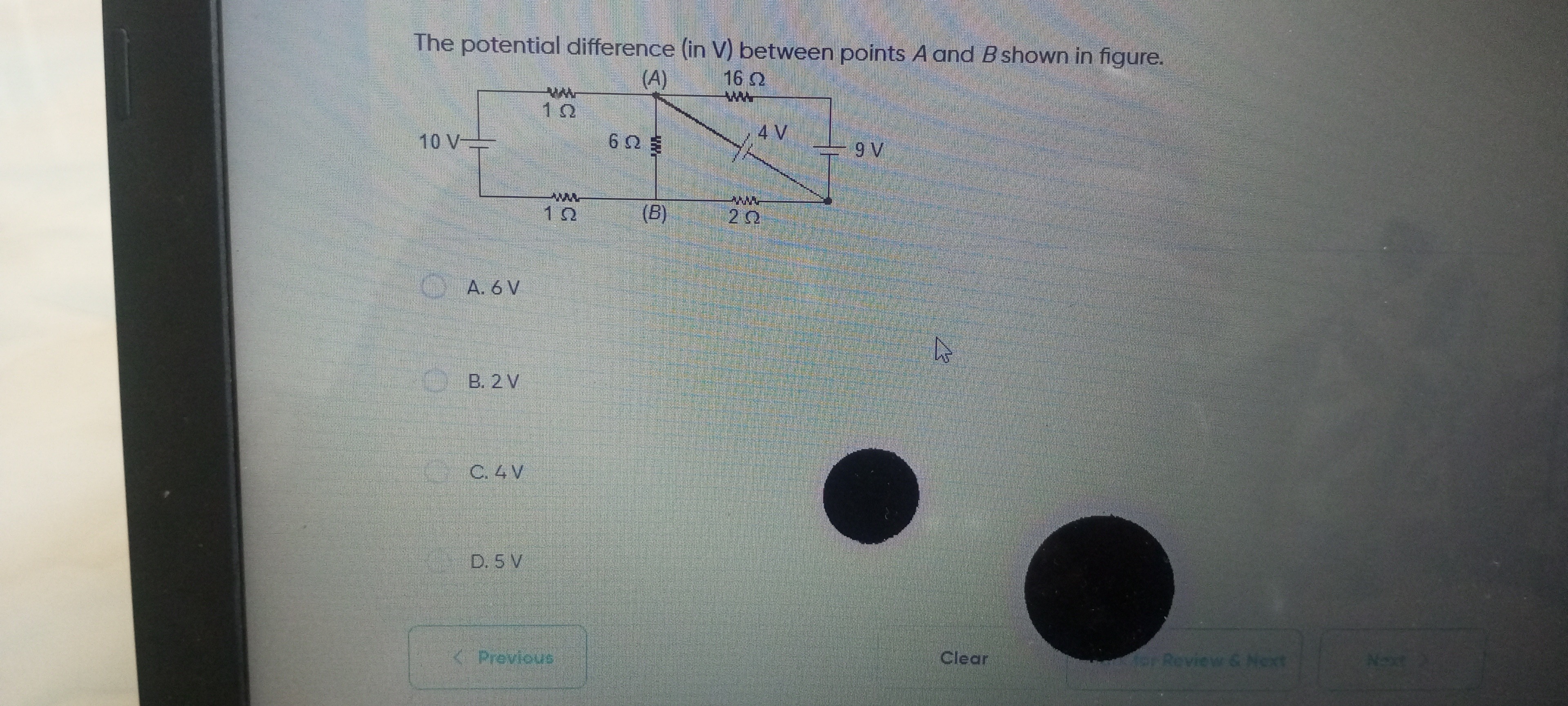
6 V
2 V
4 V
5 V
None of the options
Solution
-
Nodal Analysis Setup: Define the potential of the bottom wire as VB. Define the potential at point A as VA. The objective is to find VAB=VA−VB.
-
Express other node potentials:
- Node left of top 1Ω resistor: VB+10 V (due to 10 V battery connected to VB).
- Node right of 16Ω resistor: VB+9 V (due to 9 V battery connected to VB).
- Node between 4V battery and 2Ω resistor (VY): VA−4 V (due to 4 V battery with positive terminal at A).
-
Apply KCL at Node A: Sum of currents leaving node A is zero.
- Current through 1Ω: (VA−(VB+10))/1
- Current through 6Ω: (VA−VB)/6
- Current through 16Ω: (VA−(VB+9))/16
- Current through 4V battery and 2Ω: (VY−VB)/2=((VA−4)−VB)/2
-
Formulate and Solve Equation: Substitute VAB=VA−VB into the KCL equation: (VAB−10)/1+VAB/6+(VAB−9)/16+(VAB−4)/2=0
Multiply by 48 (LCM of denominators): 48(VAB−10)+8VAB+3(VAB−9)+24(VAB−4)=0
48VAB−480+8VAB+3VAB−27+24VAB−96=0
83VAB=480+27+96
83VAB=603
VAB=603/83 V.
-
Compare with Options: 603/83≈7.265 V, which does not match any of the integer options provided (6 V, 2 V, 4 V, 5 V).
Answer: The calculated potential difference between points A and B is 603/83 V. Since this value is not among the given options, there might be an error in the question or the options provided. However, if forced to choose, none of the options are correct based on the calculation.
