Question

The potential difference between the points A and B is

A. $1.50\,{\text{V}}$
B. $2.50\,{\text{V}}$
C. $1.00\,{\text{V}}$
D. $0.5\,{\text{V}}$

Answer 1

Divide the given circuit into two loops. Use Kirchhoff’s voltage law to determine the currents through the branches of the circuit. Use expression for Ohm’s law and determine the value of potential difference across the points A and B by substituting the obtained values of the electric currents.

Formula used:
The expression for Ohm’s law is
$V = IR$
Here, is the potential difference between the ends of a conductor, is the current in the conductor and is the resistance offered by the conductor.

Complete step by step answer:
We have given a circuit consisting of various resistors and we have asked to determine the potential difference between the points A and B. We can determine the potential difference between the points A and B using Kirchhoff’s voltage law. Kirchhoff's voltage law states that the algebraic sum of all potentials inside a loop including emf’s and the resistance elements is zero. Let us first divide the given circuit diagram in two loops as follows:

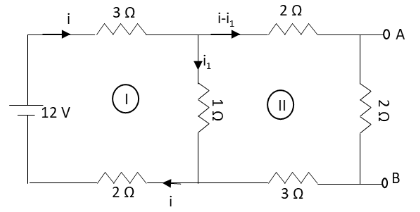
In the above circuit diagram, $i$ is the current from the battery and ${i_1}$ and $i - {i_1}$ are the branched currents flowing through the loops of the circuit.
Apply Kirchhoff’s voltage law to the first loop in the circuit.
$- 12 + 3i + 1{i_1} + 2i = 0$
$\Rightarrow - 12 + 5i + 1{i_1} = 0$
$\Rightarrow 5i + 1{i_1} = 12$ …… (1)

Apply Kirchhoff’s voltage law to the second loop in the circuit.
$2\left( {i - {i_1}} \right) + 2\left( {i - {i_1}} \right) + 3\left( {i - {i_1}} \right) - {i_1} = 0$
$\Rightarrow 7\left( {i - {i_1}} \right) - {i_1} = 0$
$\Rightarrow 7i - 7{i_1} - {i_1} = 0$
$\Rightarrow 7i - 8{i_1} = 0$ …… (2)

Multiply equation (1) by 8.
$40i + 8{i_1} = 96$
Add equation (2) in the above equation.
$\Rightarrow 40i - 8{i_1} + \left( {7i + 8{i_1}} \right) = 96$
$\Rightarrow 47i = 96$
$\Rightarrow i = \dfrac{{96}}{{47}}$
$\Rightarrow i = 2.04\,{\text{A}}$

Substitute $2.04\,{\text{A}}$ for $i$ in equation (1).
$\Rightarrow 5\left( {2.04\,{\text{A}}} \right) + 1{i_1} = 12$
$\Rightarrow 10.2 + 1{i_1} = 12$
$\Rightarrow {i_1} = 12 - 10.2$
$\Rightarrow {i_1} = 1.8\,{\text{A}}$
Hence, we have determined the values of currents flowing in the given circuit.

Now let us determine the potential difference between the points A and B. From the circuit diagram, we can see that the potential difference across points A and B is due to the resistance $2\,\Omega$ and current $i - {i_1}$ in that arm.
Rewrite Ohm’s law for this potential difference ${V_{AB}}$.
${V_{AB}} = \left( {i - {i_1}} \right)\left( {2\,\Omega } \right)$
Substitute $2.04\,{\text{A}}$ for $i$ and $1.8\,{\text{A}}$ for ${i_1}$ in the above equation.
${V_{AB}} = \left( {2.04\,{\text{A}} - 1.8\,{\text{A}}} \right)\left( {2\,\Omega } \right)$
$\Rightarrow {V_{AB}} = 0.48\,{\text{V}}$
$\therefore{V_{AB}} \approx 0.5\,{\text{V}}$
Therefore, potential difference across points A and B is $0.5\,{\text{V}}$.

Hence, the correct option is D.

Note: The students should be careful while applying Kirchhoff’s voltage law to the loops because if the signs of the potentials according to the direction of electric current is not taken properly the final values of electric currents will be incorrect and hence the resulting value of potential difference will also be incorrect.