Question
Question: The potential difference between point B and C of the circuit is- (A)\[\dfrac{{\left( {{C_2} - {C_...
The potential difference between point B and C of the circuit is-
(A)V(C2−C1)
(B)V(C4−C3)
(C) (C1+C2+C3+C4)(C2C3−C1C4).V
(D) (C1+C2)×(C3+C4)(C1C4−C2C3).V
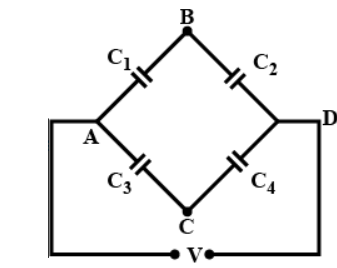
Solution
As We know when capacitors are connected in series then the total capacitance will be the reciprocal of the individual capacitors that are connected. When the capacitors are connected in parallel combination then the total capacitance is the direct addition of the individual capacitances.
CS1=C11+C21+C31+−−
CP=C1+C2+C3+−−−
Complete step by step answer:
In the arm ABD, the net voltage drop is equal to v volts and C1 and C2 are connected in series. So, the value of capacitance is-
C1=C11+C21
C=(C1+C2)C1C2
Charge will also be the same in series combination. So, Q=CV
Voltage across C2 will be = \Delta V$$$$ = \dfrac{Q}{{{C_2}}}
Here put the value of Q,
We get-ΔV=C2CV
Substitute the value of C in this equation.
ΔV=C1+C2C1V
VB−VD=C1+C2C1V
As we know potential at point D is 0. So
VB−0=C1+C2C1V
Similarly we can write, Vc−0=C3+C4C3V
Now we will calculate VB−VC ,
{V_B} - {V_C}$$$$ = \dfrac{{{C_1}V}}{{{C_1} + {C_2}}} - \dfrac{{{C_3}V}}{{{C_3} + {C_4}}}
=(C3+C4)(C1+C2)V(C1C4−C3C2)
So, potential difference between point B and C is=(C3+C4)(C1+C2)V(C1C4−C3C2).
So, the correct answer is “Option D”.
Note:
A capacitor is a device which is used to store electrical energy and charge which are available in many shapes and sizes. The amount of storage in a capacitor is calculated by a property named capacitance. There are two types of capacitance- Self capacitance and mutual conductance
The potential difference between two points is defined as the change in potential energy of a chargeq moved from one point to another. Units of potential difference are joules per Coulomb.
