Question

The potential difference between A and C if the potential difference between A and B at a certain instant is 12V.

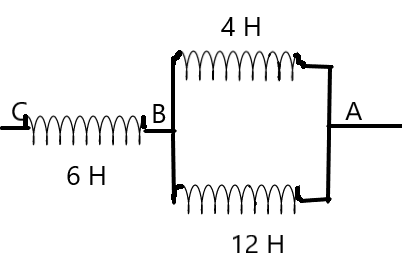
A) 12V
B) 24V
C) 36V
D) Zero

Answer 1

The relation between the potential difference, the current, and the inductance of the inductors should be used to solve the problem. The division of potential difference and division of current in a circuit need to be appropriately used.

Complete step-by-step solution
The inductance is the property of a coil to store energy in the form of a magnetic field. It can conduct only when there is a change in the emf provided until it gets charged. The rate of change of current is taken into account as a constant current usually doesn’t have a role in the inductors.
The potential difference across an inductor is given as the product of its inductance and the rate of change of current through it. It is given by –
$V=L\dfrac{dI}{dt}$

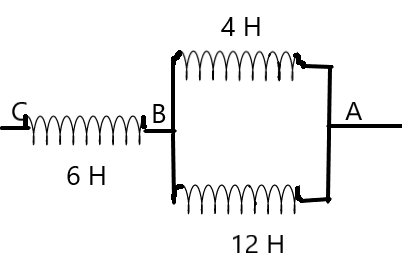
Now, we know that the potential difference across the points A and B is 12V. We can see from the figure that the two inductors of 4 H and 12 H inductance are connected parallel to each other. The potential difference across both these inductors are equal for this reason. But the current will be different. We can equate the potential difference with the rate of change of current in both cases as –

& V=L\dfrac{dI}{dt} \\\ & \Rightarrow 4\dfrac{d{{I}_{1}}}{dt}=12V\text{ } \\\ & \Rightarrow \dfrac{d{{I}_{1}}}{dt}\text{=}\dfrac{12}{4}\text{=3A}{{\text{s}}^{-1}}\text{ -(1)} \\\ & \text{and}\text{.} \\\ & \Rightarrow \text{12}\dfrac{d{{I}_{2}}}{dt}=12V \\\ & \Rightarrow \dfrac{d{{I}_{2}}}{dt}=\dfrac{12}{12}\text{=1A}{{\text{s}}^{-1}}\text{ -(2)} \\\ \end{aligned}$$ We know that the total rate of change of current through AB and AC will be the same. The rate of change of current through AB is given as – $$\begin{aligned} & \dfrac{d{{I}_{1}}}{dt}+\dfrac{d{{I}_{2}}}{dt}=3+1 \\\ & \Rightarrow \dfrac{dI}{dt}=4A{{s}^{-1}} \\\ \end{aligned}$$ Now, we know that the rate of change of current in BC is also the same as above. We can find the potential difference in BC as – $$\begin{aligned} & V=L\dfrac{dI}{dt} \\\ & \Rightarrow V=6\times 4=24V \\\ \end{aligned}$$ Now, the potential difference across AC is the sum total of the potential difference across AB and BC, which is given as – $$\begin{aligned} & {{V}_{AC}}={{V}_{AB}}+{{V}_{BC}} \\\ & \Rightarrow {{V}_{AC}}=12V+24V \\\ & \therefore {{V}_{AC}}=36V \\\ \end{aligned}$$ **The potential difference across the points A and C is 36V. The correct answer is option C.** **Note:** The potential difference across elements in a series circuit is the sum total of potential difference across each of the elements. The current, on the other hand, is a constant for the elements in a series combination. This is the opposite in the case of parallel networks.