Question

The potential difference across the terminals of a battery is $10V$ when there is a current of $3A$ in the battery from the negative to the positive terminal. When the current is $2A$ in the reverse direction, the potential difference becomes $15V$ , the internal resistance of the battery is
\left( A \right)2.5\Omega \\\ \left( B \right)5\Omega \\\ \left( C \right)2.83\Omega \\\ \left( D \right)1.0\Omega \\\

Answer 1

In order to solve this question, we are going to take a terminal with the resistor and battery. Then by taking the Kirchhoff’s voltage law, we are going to consider the two cases with the two different values of the current and voltage. The equations are mutually solved for the internal resistance.
According to the Kirchhoff’s voltage law:
${V_A} - E + IR = {V_B}$

Complete step by step solution:
Let us consider a cell $AB$ containing the resistance $r$ and battery $E$ , as shown below in the figure

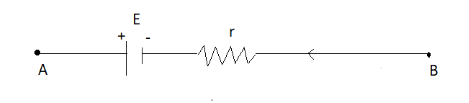
Here if we apply the Kirchhoff’s voltage law, we get the following equations:
${V_A} - E + IR = {V_B}$
On rearranging the terms in this equation, we get
${V_A} - {V_B} = E - IR$
It is given that the potential difference across the terminals is $10V$ when the current flowing is $3A$, so, taking this situation, we get
${V_A} - {V_B} = 10V$
Also, $I = 3A$
Thus, the equation becomes
$10 = E - 3r - - - \left( 1 \right)$
Now. After some time, when the current is $2A$ in the reverse direction, the potential difference becomes $15V$ ,
${V_A} - {V_B} = 15V$
$I = 2A$
Putting these values in the equation ${V_A} - {V_B} = E - IR$ , we get
$15 = E + 2r - - - \left( 2 \right)$
Subtracting equation $\left( 2 \right)$ from $\left( 1 \right)$
$\left( {E - 3r} \right) - \left( {E + 2r} \right) = 10 - 15$
$\Rightarrow - 5r = - 5$
$\Rightarrow r = 1$
Therefore, the internal resistance is $1\Omega$ .
Hence, option $\left( D \right)1.0\Omega$ is the correct answer.

Note:
Here, the current and voltage are the variable measurements varying with the change in each other’s values, however, the internal resistance of the circuit remains constant. Hence the two equations are easily formed for the solution of value of internal resistance.