Question

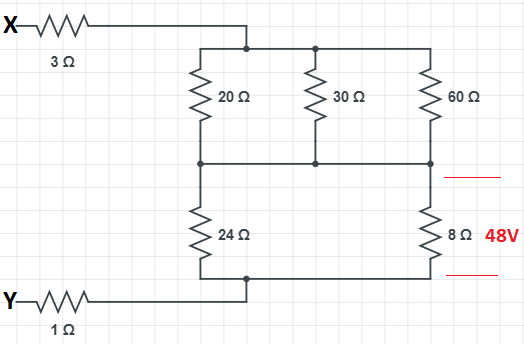
The potential difference across $8\Omega$ resistance is $48V$ as shown in the figure. The value of potential difference across $X$ and $Y$ points will be

(A) $128V$
(B) $160V$
(C) $80V$
(D) $62V$

Answer 1

In the given circuit the resistors are connected in both parallel and series connection from the point X to the point Y. In this connection a particular parallel connection has a potential difference of $48V$. We have to find the net potential difference across X and Y. Find the current through the circuit using the given potential difference across the parallel connection and also find the net resistance across X and Y. Now we have the net current and the net resistance across X and Y. Apply ohm’s law to find the net potential.

Complete step by step answer:
Given,
In the given circuit, the below mentioned resistors are connected in parallel

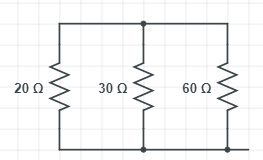
Here,
${R_{P1}} = 20\Omega$
${R_{P2}} = 30\Omega$
${R_{P3}} = 60\Omega$
The total resistance of the above circuit is ${R_p}$
The total resistance of the resistors connected parallel is given by
$\Rightarrow \dfrac{1}{{{R_P}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}}$
$\Rightarrow \dfrac{1}{{{R_P}}} = \dfrac{1}{{20}} + \dfrac{1}{{30}} + \dfrac{1}{{60}}$
$\Rightarrow \dfrac{1}{{{R_P}}} = \dfrac{3}{{60}} + \dfrac{2}{{60}} + \dfrac{1}{{60}}$
$\Rightarrow \dfrac{1}{{{R_P}}} = \dfrac{6}{{60}}$
$\Rightarrow \dfrac{1}{{{R_{P1}}}} = \dfrac{1}{{10}}$
$\Rightarrow {R_{P1}} = 10$
In the given circuit, the below mentioned resistors are also connected in parallel.

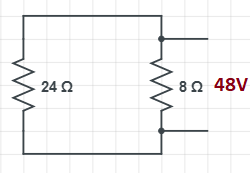
Here,
${R_{P1}} = 24\Omega$
${R_{P2}} = 8\Omega$
$\Rightarrow \dfrac{1}{{{R_P}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
$\Rightarrow \dfrac{1}{{{R_P}}} = \dfrac{1}{{24}} + \dfrac{1}{8}$
$\Rightarrow \dfrac{1}{{{R_P}}} = \dfrac{1}{{24}} + \dfrac{3}{{24}}$
$\Rightarrow \dfrac{1}{{{R_P}}} = \dfrac{4}{{24}}$
$\Rightarrow \dfrac{1}{{{R_{P2}}}} = \dfrac{1}{6}$
$\Rightarrow {R_{P2}} = 6$
And also,
Given that the potential difference across $8\Omega$ is $48V$
Since ${R_{P2}} = 8\Omega$ and ${R_{P1}} = 24\Omega$ are connected in parallel the potential difference $48V$ is applied to both the resistors, we found the net resistance of this resistor circuit
$\Rightarrow {R_{P2}} = 6$
Given, $V = 48V$
According to ohm’s law we know that
$\Rightarrow V = IR$
$\Rightarrow I = \dfrac{V}{R}$
Substitute the given values
$\Rightarrow I = \dfrac{{48}}{6}$
$\Rightarrow I = 8A$
The current through the circuit is $I = 8A$
And the circuit becomes

The resistors are in series connection
The total resistance of the resistors connected parallel is given by
$\Rightarrow {R_S} = {R_1} + {R_2} + {R_3} + ... + {R_n}$
$\Rightarrow {R_S} = {R_{S1}} + {R_{P1}} + {R_{P2}} + {R_{S2}}$
$\Rightarrow {R_S} = 3 + 10 + 6 + 1$
$\Rightarrow {R_S} = 20$
The total resistance across X and Y is ${R_S} = 20$
The current through the circuit is $I = 8A$
The potential difference across X and Y is given by the ohm’s law
$\Rightarrow V = IR$
$\Rightarrow V = 8 \times 20$
$\Rightarrow V = 160V$

Hence the correct answer is option (B), $160V$.

Note: Ohm’s law states that at constant temperature the potential difference across the conductor is proportional to the steady current flowing through the conductor.
$\Rightarrow V \propto I$
$\Rightarrow V = IR$
$V$ is the potential difference
$I$ is the current
$R$ is the resistance