Solveeit Logo
Login

Question

Question: The potential at a point P due to an electric dipole is \(1.8 \times {10^5}V\). If P is at a distanc...

The potential at a point P due to an electric dipole is 1.8×105V1.8 \times {10^5}V. If P is at a distance of 50cm apart from the centre O of the dipole and if CP makes an angle 60∘{60^ \circ } with the positive side of the axial line of the dipole, what is the moment of dipole?
A. 10C−m10C - m
B. 10−3C−m{10^{ - 3}}C - m
C. 10−4C−m{10^{ - 4}}C - m
D. 10−5C−m{10^{ - 5}}C - m

Explanation

Solution

The electric dipole is a system of two charges that are separated by a finite distance. The dipole has a property called dipole moment which is equal to the product of the charges and the distance of separation among them. It is measured in debye (D) in atomic physics and chemistry and in regular, the SI unit is used which is coulomb-metre (C-m)

Complete step-by-step answer:
The dipole has a property called dipole moment which is equal to the product of the charges and the distance of separation among them.
Consider an electric dipole of charges +q and -q separated by a distance d and a point P at a distance of r from the center and at angle θ\theta .

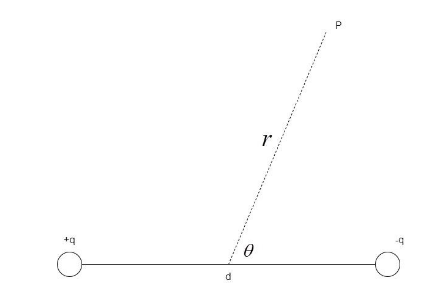
The electric potential at the point P in the figure, is given by the formula –
V=14πε0pcos⁡θr2V = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{p\cos \theta }}{{{r^2}}}
where
ε0{\varepsilon _0} = permittivity
pp = dipole moment
θ\theta = angle made by the line joining the center of dipole and the point
r = distance of the point P from the center of dipole

Given data –
Potential at the point, V=1.8×105VV = 1.8 \times {10^5}V
Angle, θ=60∘\theta = {60^ \circ }
Distance of the point P, r=50cm=0.5mr = 50cm = 0.5m
14πε0=9×109Nm2/C2\dfrac{1}{{4\pi {\varepsilon _0}}} = 9 \times {10^9}N{m^2}/{C^2}
The electric potential at the point P, V=14πε0pcos⁡θr2V = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{p\cos \theta }}{{{r^2}}}
Substituting and rearranging the equation, we get –

1.8×105=9×109×pcos⁡60∘0.52 pcos⁡60∘=1.8×105×0.529×109 Solving, pcos⁡60∘=0.05×105−9 →pcos⁡60∘=5×10−6 →p(12)=5×10−6(∵cos⁡60=12) →p=10×10−6=10−5C−m  1.8 \times {10^5} = 9 \times {10^9} \times \dfrac{{p\cos {{60}^ \circ }}}{{{{0.5}^2}}} \\\ p\cos {60^ \circ } = \dfrac{{1.8 \times {{10}^5} \times {{0.5}^2}}}{{9 \times {{10}^9}}} \\\ Solving, \\\ p\cos {60^ \circ } = 0.05 \times {10^{5 - 9}} \\\ \to p\cos {60^ \circ } = 5 \times {10^{ - 6}} \\\ \to p\left( {\dfrac{1}{2}} \right) = 5 \times {10^{ - 6}}(\because \cos 60 = \dfrac{1}{2}) \\\ \to p = 10 \times {10^{ - 6}} = {10^{ - 5}}C - m \\\

The dipole moment = 10−5C−m{10^{ - 5}}C - m

Hence, the correct option is Option D.

Note: The maximum and minimum values of the potential are determined by cos⁡θ\cos \theta
When θ=0∘→cos⁡θ=1\theta = {0^ \circ } \to \cos \theta = 1 . The electric potential will be maximum at the dipole axis.
When θ=90∘→cos⁡θ=0\theta = {90^ \circ } \to \cos \theta = 0 . The electric potential will be zero at the perpendicular axis of the dipole.