Question

The possible values of m such that the line y = mx + 4 cuts circles ${{x}^{2}}+{{y}^{2}}-4x=32$, but not circle ${{x}^{2}}+{{y}^{2}}=4$ lies in the interval:
(a) $-\sqrt{3} < m < \sqrt{3}$
(b) $-\sqrt{3}\le m\le \sqrt{3}$
(c) $m<-\sqrt{3}$ or $m>\sqrt{3}$
(d) $m\le -\sqrt{3}$ or $m\ge \sqrt{3}$

Answer 1

We will first draw a figure to understand the given conditions. It is given that the line intersects one circle but doesn’t intersect the other. This means, the point of intersection between the line and the first circle will exist and will be real and there will be no such point of intersection between the line and the second circle. To find the points, we will solve the equation of the line and the circle. We know that if a line intersects a circle, on solving we get a quadratic equation. We can find the nature of the roots by the expression ${{b}^{2}}-4ac$. If the value of the expression is greater than 0, the roots are real and unique, if the value of the expression is 0, the roots will be equal and if the value is less than 0, the roots are imaginary. Thus, we will apply the condition of imaginary roots and find the range of m.

Complete step by step answer:
The line given to us is y = mx + c and the two circles are ${{x}^{2}}+{{y}^{2}}-4x=32$ and ${{x}^{2}}+{{y}^{2}}=4$.
It is given that the line intersects the circle ${{x}^{2}}+{{y}^{2}}-4x=32$ and does not intersect ${{x}^{2}}+{{y}^{2}}=4$.
The figure according to the conditions is as follows:

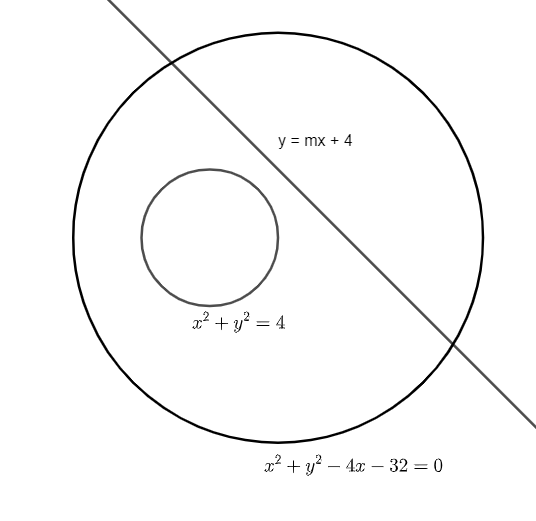
Now, we shall solve the equation of the line and the equation of the bigger circle. Thus, substitute $y=mx+4$ in equation ${{x}^{2}}+{{y}^{2}}-4x=32$.

& \Rightarrow {{x}^{2}}+{{\left( mx+4 \right)}^{2}}-4x=32 \\\ & \Rightarrow {{x}^{2}}+{{m}^{2}}{{x}^{2}}+16+8mx-4x-32=0 \\\ & \Rightarrow {{x}^{2}}\left( 1+{{m}^{2}} \right)+x\left( 8m-4 \right)-16=0 \\\ \end{aligned}$$ For the line to intersect the circle, the roots of the equation are real and unique. Thus, we will use the expression ${{b}^{2}}-4ac>0$ $\Rightarrow {{\left( 8m-4 \right)}^{2}}+4\left( 1+{{m}^{2}} \right)16>0$ For every value of m, the given inequality is true. Thus, $m\in R$. Now, we will solve the line and the smaller circle. Thus, we will substitute $y=mx+4$ in the equation ${{x}^{2}}+{{y}^{2}}=4$. $\begin{aligned} & \Rightarrow {{x}^{2}}+{{\left( mx+4 \right)}^{2}}=4 \\\ & \Rightarrow {{x}^{2}}+{{m}^{2}}{{x}^{2}}+16+8mx=4 \\\ & \Rightarrow {{x}^{2}}\left( 1+{{m}^{2}} \right)+8mx+12=0 \\\ \end{aligned}$ It is given that the circle and line does not intersect. Thus, the roots of this equation must be imaginary. So, for imaginary roots we will use the expression ${{b}^{2}}-4ac<0$ $\begin{aligned} & \Rightarrow 64{{m}^{2}}-4\left( 1+{{m}^{2}} \right)12 < 0 \\\ & \Rightarrow 4{{m}^{2}}-3-3{{m}^{2}} < 0 \\\ & \Rightarrow {{m}^{2}} < 3 \\\ & \Rightarrow -\sqrt{3} < m <\sqrt{3} \\\ \end{aligned}$ **So, the correct answer is “Option A”.** **Note:** We know that if a line intersects a circle, on solving we get a quadratic equation. If the roots of the quadratic equation are real and unique, the line intersects the circle at two points, if the roots of the quadratic equation are real and equal, the line is tangent to the circle and has one common point. If the roots are not real, the line does not intersect the circle.