Solveeit Logo
Login

Question

Question: The position \( (x) \) of a moving particle along \( x \) -axis varies with time \( (t) \) as shown ...

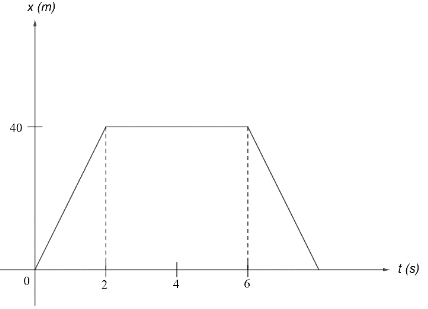
The position (x)(x) of a moving particle along xx -axis varies with time (t)(t) as shown in the figure. The average acceleration of a particle in time interval t=0t=0 to t=8st=8s is.

(A) 3ms−23m{{s}^{-2}}
(B) −5ms−2-5m{{s}^{-2}}
(C) −4ms−2-4m{{s}^{-2}}
(D) 2.5ms−22.5m{{s}^{-2}}

Explanation

Solution

Hint : Acceleration is defined as the rate of change of velocity or change in velocity per unit time. The average acceleration can be calculated by taking the difference of the final and the initial velocity divided by the total time.

Complete Step By Step Answer:
Let us observe and understand the graph and note down the data that can be obtained from it;
At time t=0st=0s , the object is at x1=0mx_1=0m
At time t=2st=2s , the object is at x2=40mx_2=40m
Hence, the object covered the distance d=40m−0md=40m-0m in time t=2s−0st=2s-0s
Now, we know that the distance traveled or displacement per unit time is defined as the velocity
Thus, the initial velocity can be calculated as,
vi=x2−x1t2−t1{{v}_{i}}=\dfrac{{{x}_{2}}-{{x}_{1}}}{{{t}_{2}}-{{t}_{1}}}
Substituting the given values,
vi=40m−0m2s−0s{{v}_{i}}=\dfrac{40m-0m}{2s-0s}
vi=40m2s{{v}_{i}}=\dfrac{40m}{2s}
Hence, the initial velocity is,
vi=20ms−1{{v}_{i}}=20m{{s}^{-1}}
Now, from the graph, for time t=2st=2s to t=6st=6s , the object remains at the position x2=40mx_2=40m .
Hence, as the position does not change, the object is said to be at rest and the velocity is zero.
From the graph,
At time t=6st=6s , the object is at x1=40mx_1=40m
At time t=8st=8s , the object is at x2=0mx_2=0m
Hence, the object causes displacement d=0m−40md=0m-40m in time t=8s−6st=8s-6s
Thus, the final velocity can be calculated as,
vf=x2−x1t2−t1{{v}_{f}}=\dfrac{{{x}_{2}}-{{x}_{1}}}{{{t}_{2}}-{{t}_{1}}}
Substituting the given values,
vf=0m−40m8s−6s{{v}_{f}}=\dfrac{0m-40m}{8s-6s}
vf=−40m2s{{v}_{f}}=\dfrac{-40m}{2s}
Hence, the final velocity is,
vf=−20ms−1{{v}_{f}}=-20m{{s}^{-1}}
Now, here we need to find the average acceleration of the object. Hence, we only need to consider the initial and final velocity of the object.
Hence, the average acceleration can be given as,
a=vf−vita=\dfrac{{{v}_{f}}-{{v}_{i}}}{t}
Substituting the given values,
∴a=−20ms−1−20ms−18s\therefore a=\dfrac{-20m{{s}^{-1}}-20m{{s}^{-1}}}{8s}
∴a=−40ms−18s\therefore a=\dfrac{-40m{{s}^{-1}}}{8s}
Hence, the average acceleration is given as,
∴a=−5ms−2\therefore a=-5m{{s}^{-2}}
Hence, the correct answer is Option (B)(B) .

Note :
To solve the problems with the graphical representation of the motion, we must have a clear understanding of the values that can be obtained by finding slopes of straight lines or by finding the area under the curve. For example, for a velocity versus time graph, the slope of a line gives the acceleration of the object, while the area under the curve gives the total displacement of the object.