Question

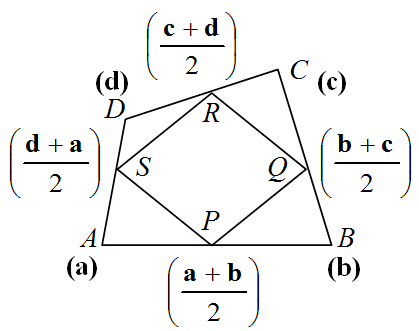
The position vectors of the vertices of a quadrilateral ABCD are a, b, c and d respectively. Area of the quadrilateral formed by joining the middle points of its sides is

• A. $\frac{1}{4}|\mathbf{a} \times \mathbf{b} + \mathbf{b} \times \mathbf{d} + \mathbf{d} \times \mathbf{a}|$
• B. $\frac{1}{4}|\mathbf{b} \times \mathbf{c} + \mathbf{c} \times \mathbf{d} + \mathbf{a} \times \mathbf{d} + \mathbf{b} \times \mathbf{a}|$
• C. $\frac{1}{4}|\mathbf{a} \times \mathbf{b} + \mathbf{b} \times \mathbf{c} + \mathbf{c} \times \mathbf{d} + \mathbf{d} \times \mathbf{a}|$
• D. $\frac{1}{4}|\mathbf{b} \times \mathbf{c} + \mathbf{c} \times \mathbf{d} + \mathbf{d} \times \mathbf{b}|$

Answer 1

Answer: (C)

$\frac{1}{4}|\mathbf{a} \times \mathbf{b} + \mathbf{b} \times \mathbf{c} + \mathbf{c} \times \mathbf{d} + \mathbf{d} \times \mathbf{a}|$

Answer 2

Let P, Q, R, S be the middle points of the sides of the quadrilateral ABCD.

Position vector of P = $\frac{\mathbf{a} + \mathbf{b}}{2}$, that of $Q = \frac{\mathbf{b} + \mathbf{c}}{2}$, that of

R = $\frac{\mathbf{c} + \mathbf{d}}{2}$ and that of S = $\frac{\mathbf{d} + \mathbf{a}}{2}$

$\left( \frac { \mathbf { c } + \mathbf { d } } { 2 } \right)$Mid point of diagonal

$SQ \equiv \left( \frac{\mathbf{d} + \mathbf{a}}{2} + \frac{\mathbf{b} + \mathbf{c}}{2} \right)\frac{1}{2} = \frac{1}{4}(\mathbf{a} + \mathbf{b} + \mathbf{c} + \mathbf{d})$ Similarly mid point of PR $\equiv \frac{1}{4}(\mathbf{a} + \mathbf{b} + \mathbf{c} + \mathbf{d})$

As the diagonals bisect each other, PQRS is a parallelogram.

$\overset{\rightarrow}{SP} = \frac{\mathbf{a} + \mathbf{b}}{2} - \frac{\mathbf{d} + \mathbf{a}}{2} = \frac{\mathbf{b} - \mathbf{d}}{2}$;

$\overset{\rightarrow}{SR} = \frac{\mathbf{c} + \mathbf{d}}{2} - \frac{\mathbf{d} + \mathbf{a}}{2} = \frac{\mathbf{c} - \mathbf{a}}{2}$

Area of parallelogram PQRS = $|\overset{\rightarrow}{SP} \times \overset{\rightarrow}{SR}| = \left| \left( \frac{\mathbf{b} - \mathbf{d}}{2} \right) \times \left( \frac{\mathbf{c} - \mathbf{a}}{2} \right) \right|$

=$\frac{1}{4}\left| \mathbf{b} \times \mathbf{c} - \mathbf{b} \times \mathbf{a} - \mathbf{d} \times \mathbf{c} + \mathbf{d} \times \mathbf{a} \right|$= $\frac{1}{4}\left| \mathbf{a} \times \mathbf{b} + \mathbf{b} \times \mathbf{c} + \mathbf{c} \times \mathbf{d} + \mathbf{d} \times \mathbf{a} \right|$