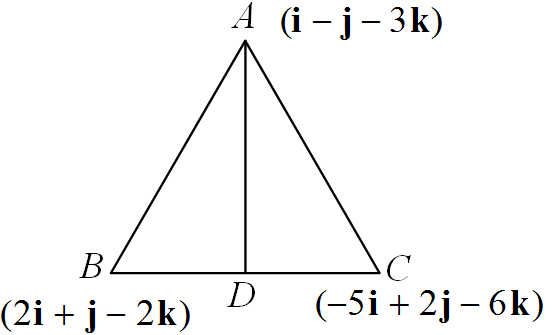Question

The position vectors of the vertices A, B, C of a triangle are $\mathbf { i } - \mathbf { j } - 3 \mathbf { k }$ , $2 \mathbf { i } + \mathbf { j } - 2 \mathbf { k }$ and $- 5 \mathbf { i } + 2 \mathbf { j } - 6 \mathbf { k }$ respectively. The length of the bisector AD of the angle BAC where D is on the segment BC, is

• A. $\frac { 3 } { 4 } \sqrt { 10 }$
• B. $\frac { 1 } { 4 }$
• C. $\frac { 11 } { 2 }$
• D. None of these

Answer 1

Answer: (A)

$\frac { 3 } { 4 } \sqrt { 10 }$

Answer 2

$| \overrightarrow { A B } | = | ( 2 \mathbf { i } + \mathbf { j } - 2 \mathbf { k } ) - ( \mathbf { i } - \mathbf { j } - 3 \mathbf { k } ) | = | \mathbf { i } + 2 \mathbf { j } + \mathbf { k } |$

= $\sqrt { 1 ^ { 2 } + 2 ^ { 2 } + 1 ^ { 2 } } = \sqrt { 6 }$

$| \overrightarrow { A C } | = | ( - 5 \mathbf { i } + 2 \mathbf { j } - 6 \mathbf { k } ) - ( \mathbf { i } - \mathbf { j } - 3 \mathbf { k } ) |$ $= | - 6 \hat { \mathbf { i } } + 3 \hat { \mathbf { j } } - 3 \hat { \mathbf { k } } |$

= $\sqrt { ( - 6 ) ^ { 2 } + 3 ^ { 2 } + ( - 3 ) ^ { 2 } }$

= $\sqrt { 54 } = 3 \sqrt { 6 }$ .

BD : DC = AB : AC = $\frac { \sqrt { 6 } } { 3 \sqrt { 6 } } = \frac { 1 } { 3 }$.

$\therefore$ Position vector of D =

= $\frac { 1 } { 4 } ( \mathbf { i } + 5 \mathbf { j } - 12 \mathbf { k } )$

$\therefore$ $\overrightarrow { A D } =$ position vector of D – Position vector of

A = $\frac { 1 } { 4 } ( \mathbf { i } + 5 \mathbf { j } - 12 \mathbf { k } ) - ( \mathbf { i } - \mathbf { j } - 3 \mathbf { k } )$ = $\frac { 1 } { 4 } ( - 3 \mathbf { i } + 9 \mathbf { j } ) = \frac { 3 } { 4 } ( - \mathbf { i } + 3 \mathbf { j } )$

$| \overrightarrow { A D } | = \frac { 3 } { 4 } \sqrt { ( - 1 ) ^ { 2 } + 3 ^ { 2 } } = \frac { 3 } { 4 } \sqrt { 10 }$