Question

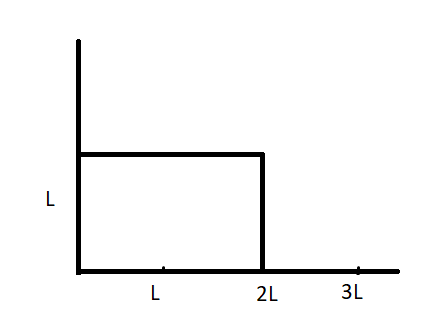
The position vector of the centre of mass $\overrightarrow r cm$ of an asymmetric uniform bar of negligible area of cross-section as shown in figure is:

A. $\overrightarrow r cm = \dfrac{{13}}{8}L\widehat x + \dfrac{5}{8}L\widehat y$
B. $\overrightarrow r cm = \dfrac{3}{8}L\widehat x + \dfrac{{11}}{8}L\widehat y$
C. $\overrightarrow r cm = \dfrac{{11}}{8}L\widehat x + \dfrac{3}{8}L\widehat y$
D. $\overrightarrow r cm = \dfrac{5}{8}L\widehat x + \dfrac{{13}}{8}L\widehat y$

Answer 1

Hint:- In this question, we can use the formula of centre of mass. We can find the $x,y$coordinates of the particles separately. After that we can substitute these values in the equation of position vector.

Complete step-by-step solution :
We know that the centre of mass of a n particle system is given as-
${x_{cm}} = \dfrac{{{m_1}{x_1} + {m_2}{x_2} + ......}}{{{m_1} + {m_2} + .....}}$ (i)
${y_{cm}} = \dfrac{{{m_1}{y_1} + {m_2}{y_2} + ......}}{{{m_1} + {m_2} + .....}}$ (ii)
Where ${m_1} + {m_2} + .....$ are the masses of the particles and ${x_1} + {x_2} + ......$ and ${y_1} + {y_2} + ......$ are the $x,y$ coordinates of the particles.
Now, from the figure,
For ${x_{cm}}$ ,
${m_1} = 2m,m{}_2 = m,{m_3} = m$ and ${x_1} = L,{x_2} = 2L,{x_3} = \dfrac{{5L}}{2}$
So, putting the above values in the equation (i), we get-
${x_{cm}} = \dfrac{{2m \times L + m \times 2L + m \times \dfrac{{5L}}{2}}}{{2m + m + m}} \\\ \Rightarrow {x_{cm}} = \dfrac{{13}}{8}L \\\$
Similarly, for ${y_{cm}}$,
${m_1} = 2m,m{}_2 = m,{m_3} = m$ and ${y_1} = L,{y_2} = \dfrac{L}{2},{y_3} = 0$
So, putting the values in the equation (ii), we get-
${y_{cm}} = \dfrac{{2m \times L + m \times \dfrac{L}{2} + m \times 0}}{{2m + m + m}} \\\ \Rightarrow {y_{cm}} = \dfrac{5}{8}L \\\$
Thus, the position vector of the centre of mass =$\dfrac{{13}}{8}L\widehat x + \dfrac{5}{8}L\widehat y$ .
Hence option A is correct.

Additional Information:-
Centre of mass is defined as the point at which the total mass of the body works. In a body, there are an infinite number of particles having different masses. We can’t calculate the mass of each particle as they are very small in size. So, we assume that at a point the total mass of the body works. In physics, all the calculations related to the motion are done with the help of centre of mass.

Note:- In this question, we have to remember the formula of centre of mass. We should also remember that the $x,y$coordinates will be found separately. The values of $x,y$are different for the same mass. We should keep in mind that the value of ${x_{cm}}$is written with $\widehat x$ and the value of ${y_{cm}}$is written with $\widehat y$.