Question

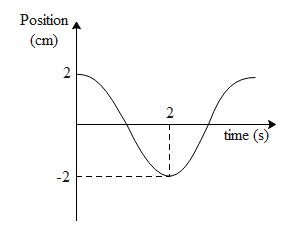
The position time graph of a particle is shown in the figure below. The magnitude of the acceleration of the particle at t = $\dfrac{2}{3}$ is ?

a) $\dfrac{{{\pi }^{2}}}{4}cm{{s}^{-2}}$
b) $\dfrac{2{{\pi }^{2}}}{4}cm{{s}^{-2}}$
c) $\dfrac{2{{\pi }^{2}}}{3\sqrt{3}}cm{{s}^{-2}}$
d) $\dfrac{3{{\pi }^{2}}}{\sqrt{3}}cm{{s}^{-2}}$

Answer 1

In the above question, the position time graph of a particle is given which is basically oscillating with time. First we need to determine the nature of the graph, the time period of oscillation and other parameters of an oscillatory system. Therefore further after obtaining the equation of motion of the particle and accordingly taking the double derivative with respect to time, will enable us to determine the acceleration of the particle at any instance of time.

Formula used:
$x=A\cos \omega t$
$a=\dfrac{{{d}^{2}}x}{d{{t}^{2}}}$

Complete step-by-step answer:
If we observe the above graph carefully, at time t= 0, the particle has a maximum amplitude. This nature is depicted by the cosine function. Hence the nature of the above graph is that of cosine. If a particle oscillates with amplitude ‘A’ and angular frequency $\omega$, then the position (x) of the particle at time ‘t’ is given by,
$x=A\cos \omega t$
If the time period of oscillation of the particle is T, then the above equation can be written as,
$x=A\cos \left( \dfrac{2\pi }{T}t \right)$
For the above graph the amplitude is equal to 2cm and the time period is 4 sec. Therefore the above equation of oscillatory motion for the above given particle is,
$\begin{aligned} & x=2cm\cos \left( \dfrac{2\pi }{4s}t \right) \\\ & \therefore x=2cm\cos \left( \dfrac{\pi }{2}t \right) \\\ \end{aligned}$
The acceleration ‘a’ of the particle is given by a double derivative of its position. Hence the acceleration of the particle is,
$\begin{aligned} & a=\dfrac{{{d}^{2}}x}{d{{t}^{2}}} \\\ & \Rightarrow a=\dfrac{{{d}^{2}}}{d{{t}^{2}}}\left( x=2cm\cos \left( \dfrac{\pi }{2}t \right) \right) \\\ & \Rightarrow a=-\dfrac{{{\pi }^{2}}}{2}cm\cos \left( \dfrac{\pi }{2}t \right) \\\ & \because t=\dfrac{2}{3}s \\\ & \Rightarrow a=-\dfrac{{{\pi }^{2}}}{2}cm\cos \left( \dfrac{\pi }{2}\left( \dfrac{2}{3} \right) \right)=-\dfrac{{{\pi }^{2}}}{2}cm\cos \left( \dfrac{\pi }{3} \right) \\\ & \because \cos \dfrac{\pi }{3}=\dfrac{1}{2} \\\ & \therefore a=-\dfrac{{{\pi }^{2}}}{4}cm{{s}^{-2}} \\\ \end{aligned}$

So, the correct answer is “Option (a)”.

Note: The amplitude of the particle is defined as the maximum displacement with respect to mean position. Similarly the time period is defined as the time taken by the particle to complete one full oscillation. It is also to be noted that the acceleration of the above is negative, which does not mean the magnitude is negative.