Question

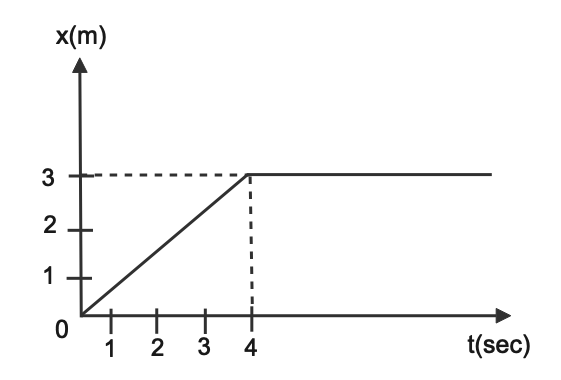
The position time graph of a body of mass 2 kg is shown in the figure what is the impulse of the body at t = 4 sec

A. 2.5 kg m/s
B. -2.5 kg m/s
C. 1.5 kg m/s
D. -1.5kg m/s

Answer 1

In order to solve the question, we will first use the graph to find out initial velocity then we will use the slope of position time to find the final velocity after then we us the formula of impulse to find out the impulse from time one second to time equal to four second.

Formula Used:
Velocity of a body in position time graph is slope of the graph
$v = \tan \theta$
$\tan \theta = \dfrac{p}{b}$
P refers to perpendicular
B refers to base
Impulse is the instantaneous change in momentum
$I = Mv - Mu$
I refer to impulse
M refers to mass
V refers to final velocity
U refers to initial velocity

Complete step by step solution:
Impulse is the change in the momentum of a body
In the question we are given the mass of the body and we have to find the impulse with the help of the position time graph given
Mass of the body = 2 kg
The body is at x = 0 when t = 0 that means body is at rest
Therefore, impulse at t = 0 and x = 0 is zero
Form t = 0 s to t = 4 s the position time graph shows the straight line, which means that the velocity of the body is uniform
Beyond t = 4s the graph is straight line parallel to time axis that means body is at rest which means velocity is zero
Now we will find the velocity
Velocity of a body in position time graph is slope of the graph
$v = \tan \theta$
$\tan \theta = \dfrac{p}{b}$
Perpendicular is 3 units from the graph
Base is 4 units from graph
$\tan \theta = \dfrac{3}{4}$
Hence final velocity is $\dfrac{3}{4}m{s^{ - 1}}$
Now we will find the impulse from t = 0s to t = 4s
Impulse is the instantaneous change in momentum
$I = Mv - Mu$
M as given is 2 kg
Final velocity we found as $\dfrac{3}{4}m{s^{ - 1}}$
Initial velocity is zero as described earlier
Taking the mass common
$I = M(v - u)$
Substituting the values
$I = 2\left( {0 - \dfrac{3}{4}} \right)$
Solving for impulse we get
$I = - \dfrac{3}{2}Kg{\text{ m}}{{\text{s}}^{ - 1}} = 1.5Kg{\text{ m}}{{\text{s}}^{ - 1}}$
Hence, the correct option is 4) -1.5kg m/s.

Note: Many of the people may confuse between impulse and collision as the object experiences the change in momentum in both the cases but the collision takes less time than impulse as impulse is the fast acting force or the impact on the object. Hence both differences because of the time period.