Question
Question: The position of point from wire ‘B’. where net magnetic field is zero due to following current distr...
The position of point from wire ‘B’. where net magnetic field is zero due to following current distribution.:
(a) 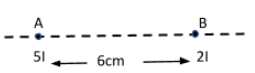
A. 76cm
B. 712cm
C. 718cm
D. 716cm
(b) 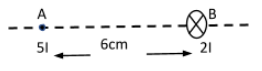
A. 4cm
B. 2cm
C. 8cm
D. 12cm
Solution
A magnetic field is a vector field that describes the magnetic influence on moving electric charges, electric current and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and to the magnetic field. The SI unit is Tesla ‘T’.
Formula used:
B=2πrμI
Here, I=current and r=distance.
Complete step by step answer:
(a)
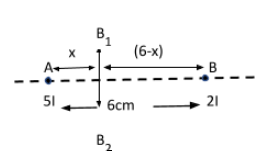
For Bnet=0
And B1=B2
As we know that
2πr1μI1=2πr2μI2
Put the values
2π×xμ×(5i)=2π×(6−x)μ×(2i)
Simplify
(5i)(6−x)=(2i)(x)
⇒30−5x=2x
⇒x=730cm
From B,
⇒(6−x)
Put the values
⇒(6−730)
⇒712cm
So the correct answer is option B.
(b)

For
Bnet=0
And B1=B2
As we know that
2πr1μI1=2πr2μI2
Put the values
2π×(6+x)μ×(5i)=2π×(x)μ×(2i)
Simplify
(5i)(x)=(2i)(6+x)
⇒5x=2x+12
∴x=4cm
So the correct answer is option A.
Note: The direction of the magnetic force on a moving charge is perpendicular to the plane formed by v and B follows right hand rule. The magnitude of the force is proportional to q,v,B and the sine of the angle between v and B. A magnetic field is imaginary lines, it only experiences.
