Solveeit Logo
Login

Question

Question: The position of final image from O for the arrangement as shown (A). \(-24cm\) (B). \(-120cm\) ...

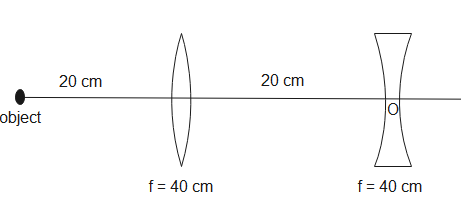
The position of final image from O for the arrangement as shown
(A). −24cm-24cm
(B). −120cm-120cm
(C). −40cm-40cm
(D). −20cm-20cm

Explanation

Solution

Two lenses are kept at a distance from each other. By refraction from the first lens, the image formed by the first lens will act as the object for the second lens. The final image is formed by the second lens. Respective distances can be calculated using lens formula which gives relation between object distance, image distance and focal length.
Formulas used:
1v−1u=1f\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}

Complete answer:
The image in lenses is formed by the phenomenon of refraction. When a light travels from one medium to another medium, it changes its path, this phenomenon is known as refraction.
Given, focal length of convex lens is 40cm40cm and the focal length of concave lens is −40cm-40cm.
The lens formula is given as-
1v−1u=1f\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f} - (1)
Here, vv is the image distance
uu is the object distance
ff is the focal length
For refraction at first surface,
u=−20cmu=-20cm, f=40cmf=40cm. Substituting given values in eq (1), we get,
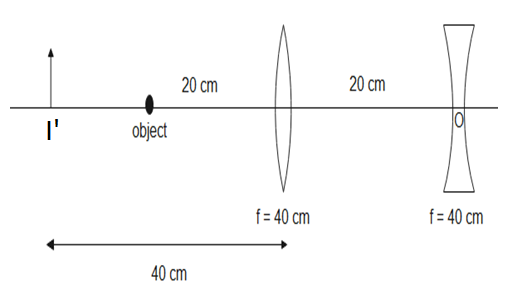
1v−1−20=140 ⇒1v+120=140 ⇒1v=140−120 ⇒1v=−140 ∴v=−40cm \begin{aligned} & \dfrac{1}{v}-\dfrac{1}{-20}=\dfrac{1}{40} \\\ & \Rightarrow \dfrac{1}{v}+\dfrac{1}{20}=\dfrac{1}{40} \\\ & \Rightarrow \dfrac{1}{v}=\dfrac{1}{40}-\dfrac{1}{20} \\\ & \Rightarrow \dfrac{1}{v}=\dfrac{-1}{40} \\\ & \therefore v=-40cm \\\ \end{aligned}

The image formed by the first lens is 40 cm behind the lens which means it is 40+20=60cm40+20=60cm behind the second lens.
Therefore, for refraction by second lens, u=−60cmu=-60cm, f=−40cmf=-40cm
Substituting given values in eq (1), we get,
1v−1−60=1−40 ⇒1v+160=−140 ⇒1v=−160−140 ⇒1v=−5120 ∴v=−24cm \begin{aligned} & \dfrac{1}{v}-\dfrac{1}{-60}=\dfrac{1}{-40} \\\ & \Rightarrow \dfrac{1}{v}+\dfrac{1}{60}=-\dfrac{1}{40} \\\ & \Rightarrow \dfrac{1}{v}=-\dfrac{1}{60}-\dfrac{1}{40} \\\ & \Rightarrow \dfrac{1}{v}=\dfrac{-5}{120} \\\ & \therefore v=-24cm \\\ \end{aligned}
Therefore, the final image is 24cm24cm away from the point O behind the lens.

Hence, the correct option is (A).

Note:
By convention, all distances measured from right to left are taken as positive and distances from left to right are taken as negative. The focal length of a convex lens is taken as positive and the focal length of a concave lens is taken as negative. The object distance is always negative. The convex lens is a converging lens while the concave lens is a diverging lens.