Question

The position of a particle moving along the x-axis is related to time / as follows: $x = 2{t^2} - {t^3}$, where x is in meters and t is in seconds. What is the maximum positive displacement of the particle along the x axis and at what instant does it attain it? Describe the motion of the particle. What is the distance covered in the first three seconds? What is its displacement in the first four seconds? What are the particles average speed and average velocity in the first 3 seconds? What are the particles' instantaneous acceleration at the instant of its maximum positive x displacement? What is the average acceleration between the interval t= 2s to t = 4s?

Answer 1

Hint We should know that displacement is defined as the change in an object’s position from the origin. To find the displacement we have to use (final position) – (initial position).

Complete step by step answer
We know that the derivative of x with respect to the time will give the velocity of the particle in the relation with the time.
$v = \dfrac{{dx}}{{dt}} = 4t - 3{t^2}............(i)$
The double derivative of x with respect to the time will give acceleration of the particle in relation with time.
$a = \dfrac{{{d^2}x}}{{d{t^2}}} = 4 - 6t..................(ii)$
For the minimum and maximum displacement, dx/dt = 0.
Thus,
${\text{Displacement from 0 to }}\dfrac{{\text{4}}}{{\text{3}}}{\text{s + Displacement from 0 to }}\dfrac{{\text{4}}}{{\text{3}}}{\text{s to 3s}}$
Also, for the maxima, double derivative of x should be negative that is:
$\dfrac{{{d^2}x}}{{d{t^2}}} < 0$
$\Rightarrow \dfrac{{{d^2}x}}{{d{t^2}}} = 4 - 6t$
At t = 0:
$\dfrac{{{d^2}x}}{{d{t^2}}} = 4 - 6(0) = 4(positive)$
And at t = (4/3 s):
$\dfrac{{{d^2}x}}{{d{t^2}}} = 4 - 6(\dfrac{4}{3}) = 4 - 8 = - 4(negative)$
Therefore, the particle is at the maximum displacement at t = $\dfrac{4}{3}s$and the corresponding displacement is ${x_{\max }} = 2{\left( {\dfrac{4}{3}} \right)^2} - {\left( {\dfrac{4}{3}} \right)^3} = \dfrac{{32}}{{37}}m$.
The maximum particle displacement of the particle is ${x_{\max }} = \dfrac{{32}}{{27}}m$and it will occur at t = $\dfrac{4}{3}s$.
Velocity is positive when v > 0 or $4t - 3{t^2} > 0$or t(4 – 3t) > 0 .
We can write this as: $t > 0,t < \dfrac{4}{3}s$
For acceleration to be positive,
$a > 0$
$\Rightarrow 4 - 6t > 0,t < \dfrac{2}{3}s$
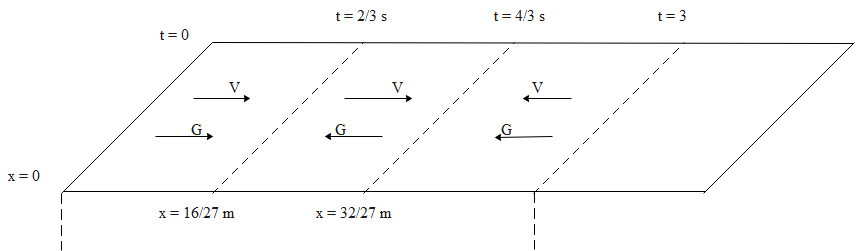
From t = 0 to $t < \dfrac{2}{3}s$, the velocity $(\vec v)$and $(\vec a)$acts in negative x-direction. Hence, the velocity of the particle decreases 4 and becomes 0 at $t = \dfrac{4}{3}s.$Then after, the particle moves in negative x-direction.
The velocity is positive between the instants 0 and 4/3 s and is negative at instant 4/3 s to the remaining 3 s.
The total distance is = ${\text{Displacement from 0 to }}\dfrac{{\text{4}}}{{\text{3}}}{\text{s + Displacement from 0 to }}\dfrac{{\text{4}}}{{\text{3}}}{\text{s to 3s}}$
That is,
$x\left( {\dfrac{4}{3}} \right) - x(0) + x(3) - x\dfrac{4}{3}$
= 2{\left( {\dfrac{4}{3}} \right)^2} - {\left( {\dfrac{4}{3}} \right)^3} - (0) + 2{(3)^2} - {(3)^2} - \left\\{ {2{{\left( {\dfrac{4}{3}} \right)}^2} - {{\left( {\dfrac{4}{3}} \right)}^3}} \right\\}
$= \dfrac{{16}}{9}\left( {2 - \dfrac{4}{3}} \right) + 9(2 - 3) - \dfrac{{16}}{9}\left( {2 - \dfrac{4}{3}} \right)$
$= \dfrac{{307}}{{27}}m$
The required displacement is the difference in the position at t = 4s and t = 0.
The diagram for the question, is given below:

Note The displacement time equation finds the original velocity multiplied by the time plus one half of the acceleration multiplied by the square if the time.