Question

The position of a particle is given by $\overrightarrow r = 3t\,\widehat i + 2{t^2}\widehat j + 5\widehat k$, where t is in seconds and the coefficients have the proper units for r to be in meters. The direction of velocity of the particle at $t = 1s$is:
A. $53^\circ \,\,with\,\,x - axis$
B. $37^\circ \,\,with\,\,x - axis$
C. $30^\circ \,\,with\,\,y - axis$
D. $60^\circ \,\,with\,\,x - axis$

Answer 1

To solve this first we need to differentiate the position of the particle with respect to time so as to get the velocity of the particle at time t. Now putting the given time period we will get the velocity vector of the particle. Now to find the direction of the velocity vector we need to calculate the angle between the two axes. Now applying the theorem formula we can calculate the angle.

Complete step by step answer:
As per the problem we know the position of a particle is given by $\overrightarrow r = 3t\,\widehat i + 2{t^2}\widehat j + 5\widehat k$, where t is in seconds and the coefficients have the proper units for r to be in meters.We need to calculate the direction of velocity of the particle at $t = 1s$.We know,
$\overrightarrow v = \dfrac{{d\overrightarrow r }}{{dt}}$

Now on differentiating position vector of particle with respect to time we will get,
$\overrightarrow r = 3t\,\widehat i + 2{t^2}\widehat j + 5\widehat k$
$\Rightarrow \overrightarrow v = \dfrac{{d\left( {3t\,\widehat i + 2{t^2}\widehat j + 5\widehat k} \right)}}{{dt}}$
On differentiating we will get,
$\overrightarrow v = 3\,\widehat i + 4t\widehat j\,\,m{s^{ - 1}}$
This shows that it has no component along the z-axis.

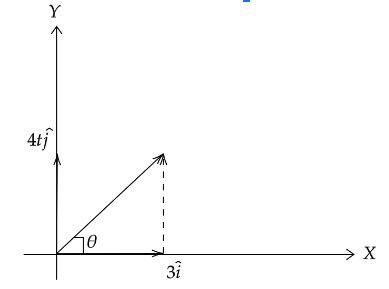
As per the diagram we can see that the resultant direction of the vector is in the positive x-axis.Now after time $t = 1s$ velocity will be,
$\overrightarrow v = 3\,\widehat i + 4\widehat j\,\,m{s^{ - 1}}$
The magnitude of the vector will be,
$|v| = \sqrt {{x^2} + {y^2}}$

Now putting the value we will get,
$|v| = \sqrt {{3^2} + {4^2}}$
$\Rightarrow |v| = 5m{s^{ - 1}}$
Let $\theta$ is the angle in which the direction of $\overrightarrow v$, takes with the x-axis.
$\tan \theta = \dfrac{y}{x}$
$\Rightarrow \theta = {\tan ^{ - 1}}\dfrac{y}{x}$
Now putting the value we will get,
$\theta = {\tan ^{ - 1}}\dfrac{4}{3}$
$\therefore \theta = 53^\circ$

Therefore the correct option is $\left( A \right)$.

Note: In this type of problem to show the component we have to represent the vectors on the coordinate axis and a vector is an element of a vector space.Note that in physics a vector is a quantity that has both magnitude and direction.