Question

The population $N(t)$ of ill patients during an epidemic in a country is given by the following equation

$N(t) = \frac{N_0 \exp(t/\tau)}{1 + N_0(\exp(t/\tau) - 1)/N_s}$

where $N_0$ is the initial population of ill patients, $N_s \gg N_0$ is a large number and $\tau$ is a positive constant. The sketch which describes it best is

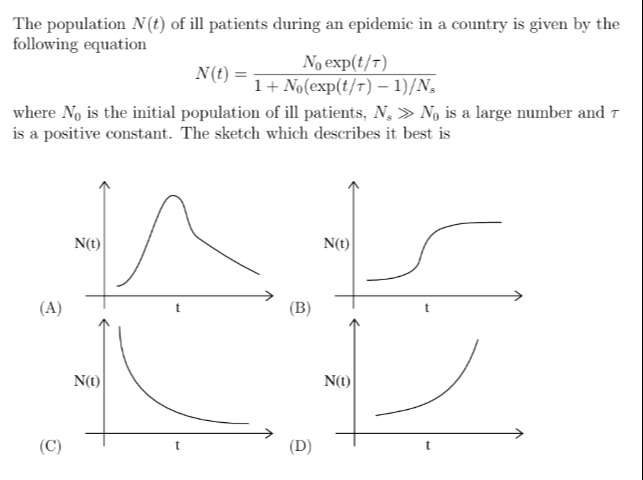
• A. Graph A shows a population that increases, reaches a peak, and then decreases.
• B. Graph B shows an S-shaped curve, starting at a positive value, increasing, and then flattening out as it approaches a saturation value.
• C. Graph C shows a decreasing population (exponential decay).
• D. Graph D shows an exponentially increasing population without any saturation.

Answer 1

Answer: (B)

Graph B shows an S-shaped curve, starting at a positive value, increasing, and then flattening out as it approaches a saturation value.

Answer 2

The given equation is a logistic function.

1. At $t=0$, $N(0) = N_0$.
2. As $t \to \infty$, $N(t)$ approaches $N_s$ (a finite saturation value).
3. The derivative $\frac{dN}{dt}$ is always positive, meaning $N(t)$ is always increasing.

These properties describe an S-shaped curve, where the population starts at $N_0$, grows, and then the growth rate slows as it approaches the carrying capacity $N_s$. Graph B depicts this behavior.