Question

The polar equation of the line passing through $(4,\dfrac{{2\pi }}{3})$ and perpendicular to the line joining the origin to this point is ?

Answer 1

Equation of a line using its distance from the normal and the angle which normal makes with positive x-axis is known. Here those two values are given. So by simply substituting we can find the equation.

Formula used:
Equation of a line at a distance $p$ from the normal and the normal make an angle $\alpha$ with the polar axis is
$r\cos (\theta - \alpha ) = p$

Complete step-by-step answer:
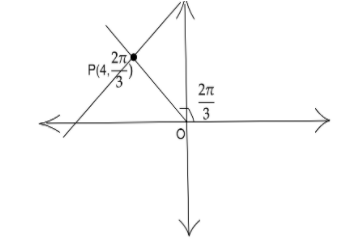
Given a point $(4,\dfrac{{2\pi }}{3})$
We have to find the polar equation of the line passing through $(4,\dfrac{{2\pi }}{3})$ and perpendicular to the line joining the origin to this point.
For a point written in polar form with the coordinates, the first coordinate represents the distance of the point from the origin and the second one represents the angle, which the line joining the point and origin, makes with the polar axis (positive x-axis).
So, we can see the given point is $4$ units away from the origin and the line joining this point and origin makes an angle $\dfrac{{2\pi }}{3}$ with the polar axis.
Equation of a line at a distance $p$ from the normal and the normal make an angle $\alpha$ with the polar axis is
$r\cos (\theta - \alpha ) = p$
So here we have, $p = 4$ and $\alpha = \dfrac{{2\pi }}{3}$
Therefore, required equation is $r\cos (\theta - \dfrac{{2\pi }}{3}) = 4$

Note: Since there are two angles $\theta$ and $\alpha$ in the equation, we may confuse one with another. Actually here $r,\theta$ are variables for the line. They take different values for different points. For each point $r$ is the distance from the origin and $\theta$ is the angle which the line joining origin and that point makes with the positive x-axis.