Question

The polar coordinates of the vertices of a triangle are $\left( 0,0 \right),\left( 3,\dfrac{\pi }{2} \right)\ and\ \left( 3,\dfrac{\pi }{6} \right)$. Then the triangle is,
A. Right angled
B. Isosceles
C. Equilateral
D. None of these

Answer 1

Hint: In the above question we will first find the all side of triangle by using the distance formula between $\left( {{x}_{1}},{{y}_{1}} \right)\ and\ \left( {{x}_{2}},{{y}_{2}} \right)$ as follows:
$D=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$
Also, we will use the formula to change the polar coordinates into Cartesian coordinates as follows:
Let, we have polar coordinates $\left( r,\theta \right)$ then in Cartesian coordinates,
X coordinates $=r\cos \theta$
Y coordinates $=r\sin \theta$

Complete step-by-step answer:

We have been given the polar coordinates of the vertices of a triangle are $\left( 0,0 \right),\left( 3,\dfrac{\pi }{2} \right)\ and\ \left( 3,\dfrac{\pi }{6} \right)$.
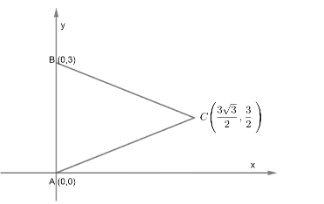
Let us suppose a $\Delta ABC$ where $A\left( 0,0 \right),B\left( 3,\dfrac{\pi }{2} \right)\ and\ C\left( 3,\dfrac{\pi }{6} \right)$.
We know that in Cartesian form the polar coordinates $\left( r,\theta \right)$ is written as;
X coordinates $=r\cos \theta$
Y coordinates $=r\sin \theta$
$B\left( 3,\dfrac{\pi }{2} \right)$
X coordinates $=3\cos \dfrac{\pi }{2}=3\times 0=0$
Y coordinates $=3\sin \dfrac{\pi }{2}=3\times 1=3$
$C\left( 3,\dfrac{\pi }{6} \right)$
X coordinates $=3\cos \dfrac{\pi }{6}=3\times \dfrac{\sqrt{3}}{2}=\dfrac{3\sqrt{3}}{2}$
Y coordinates $=3\sin \dfrac{\pi }{6}=3\times \dfrac{1}{2}=\dfrac{3}{2}$

We know that distance between two points $\left( {{x}_{1}},{{y}_{1}} \right)\ and\ \left( {{x}_{2}},{{y}_{2}} \right)$ is given by,
$D=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$
We have $A\left( 0,0 \right)\ and\ B\left( 0,3 \right)$
$\begin{aligned} & \Rightarrow AB=\sqrt{{{\left( 0-0 \right)}^{2}}+{{\left( 3-0 \right)}^{2}}} \\\ & =\sqrt{0+9} \\\ & =3 \\\ \end{aligned}$
Also, we have $A\left( 0,0 \right)\ and\ C\left( \dfrac{3\sqrt{3}}{2},\dfrac{3}{2} \right)$
$\begin{aligned} & \Rightarrow AC=\sqrt{{{\left( \dfrac{3\sqrt{3}}{2}-0 \right)}^{2}}+{{\left( \dfrac{3}{2}-0 \right)}^{2}}} \\\ & =\sqrt{\dfrac{27}{4}+\dfrac{9}{4}} \\\ & =\sqrt{\dfrac{36}{4}} \\\ & =\dfrac{6}{2} \\\ & =3 \\\ \end{aligned}$
Again, we have $B\left( 0,3 \right)\ and\ C\left( \dfrac{3\sqrt{3}}{2},\dfrac{3}{2} \right)$
$\begin{aligned} & \Rightarrow BC=\sqrt{{{\left( \dfrac{3\sqrt{3}}{2}-0 \right)}^{2}}+{{\left( \dfrac{3}{2}-0 \right)}^{2}}} \\\ & =\sqrt{\dfrac{27}{4}+{{\left( \dfrac{-3}{2} \right)}^{2}}} \\\ & =\sqrt{\dfrac{27}{4}+\dfrac{9}{4}} \\\ & =\sqrt{\dfrac{36}{4}} \\\ & =\dfrac{6}{2} \\\ & =3 \\\ \end{aligned}$
So, we get $AB=BC=AC=3unit$.
We know that if a triangle has all its sides equal then it must be an equilateral triangle.
Hence, ABC is an equilateral triangle.
Therefore, the correct option of the given question is option C.

Note: We can also find the type of triangle by finding the angles between the lines of the triangle and in that case we get each angle equal to $60{}^\circ$. Hence, it is an equilateral triangle. Also, remember that we have been given the coordinates in polar form. So, we must have to change it into Cartesian form otherwise we will make mistakes and treat it like Cartesian coordinates.