Question

The points $\left( 2,3 \right)$ , $\left( 0,2 \right)$ , $\left( 4,5 \right)$ and $\left( 0,t \right)$ are concyclic if the value of t is
(A) 2
(B) 1
(C) 17
(D) 19

Answer 1

Hint: First of all, assume that the equation of a circle is ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ . Since the points $\left( 2,3 \right)$ , $\left( 0,2 \right)$ , and $\left( 4,5 \right)$ are concyclic so, the coordinates of these points must satisfy the equation of the circle. Put the coordinates of the points $\left( 2,3 \right)$ , $\left( 0,2 \right)$ , and $\left( 4,5 \right)$ in the equation ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ and get three equations. Now, we have three equations and three variables that are g, f, and c. Now, solve it and get the values of g, f, and c, and then put the values of g, f, and c in the equation ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ . We will get the equation of the circle ${{x}^{2}}+{{y}^{2}}+5x-19y+34=0$ . Since point D $\left( 0,t \right)$ is also concyclic so it must satisfy the equation of the circle ${{x}^{2}}+{{y}^{2}}+5x-19y+34=0$ . Now, put the coordinate of point D $\left( 0,t \right)$ in the equation ${{x}^{2}}+{{y}^{2}}+5x-19y+34=0$ and get the value of t.

Complete step-by-step answer:
According to the question, we have the coordinates of three points that are concyclic and we have the coordinate of the fourth point $\left( 0,t \right)$ . We have to find the value of t such that the fourth point also becomes concyclic.
The coordinate of the point A = $\left( 2,3 \right)$ ……………………………..(1)
The coordinate of point B = $\left( 0,2 \right)$ ……………………………….(2)
The coordinate of the point C = $\left( 4,5 \right)$ ………………………………..(3)
The coordinate of the point D = $\left( 0,t \right)$ ………………………………….(4)
Let us assume the equation of the common circle is ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ .
We know that a set of points can be concyclic if they all lie on the same circle.
Since the points A, B, C, and D are concyclic so, these points must lie on the circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ .
As the points, A, B, C, and D are lying on the circle, so it must satisfy the equation of the circle.

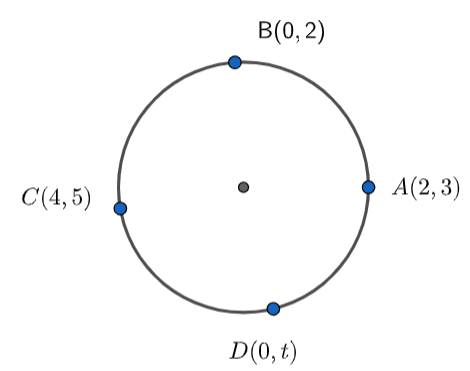
Now, putting the coordinate of the point A = $\left( 2,3 \right)$ in the equation of the circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ , we get

& {{\left( 2 \right)}^{2}}+{{\left( 3 \right)}^{2}}+2g\left( 2 \right)+2f\left( 3 \right)+c=0 \\\ & \Rightarrow 4+9+4g+6f+c=0 \\\ \end{aligned}$$ $$\Rightarrow 4g+6f+c=-13$$ ……………………………(5) Now, putting the coordinate of the point B = $$\left( 0,2 \right)$$ in the equation of the circle $${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$$ , we get $$\begin{aligned} & {{\left( 0 \right)}^{2}}+{{\left( 2 \right)}^{2}}+2g\left( 0 \right)+2f\left( 2 \right)+c=0 \\\ & \Rightarrow 0+4+4f+c=0 \\\ \end{aligned}$$ $$\Rightarrow 4f+c=-4$$ $$\Rightarrow c=-4-4f$$ ……………………………(6) Now, putting the coordinate of the point C = $$\left( 4,5 \right)$$ in the equation of the circle $${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$$ , we get $$\begin{aligned} & {{\left( 4 \right)}^{2}}+{{\left( 5 \right)}^{2}}+2g\left( 4 \right)+2f\left( 5 \right)+c=0 \\\ & \Rightarrow 16+25+8g+10f+c=0 \\\ \end{aligned}$$ $$\Rightarrow 8g+10f+c=-41$$ ……………………………(7) Now, putting the value of c from equation (6) in equation (7), we get $$\begin{aligned} & \Rightarrow 8g+10f+\left( -4-4f \right)=-41 \\\ & \Rightarrow 8g+10f-4-4f=-41 \\\ & \Rightarrow 8g+10f-4f=-41+4 \\\ \end{aligned}$$ $$\Rightarrow 8g+6f=-37$$ ……………………….(8) Now, putting the value of c from equation (6) in equation (5), we get $$\begin{aligned} & \Rightarrow 4g+6f+\left( -4-4f \right)=-13 \\\ & \Rightarrow 4g+6f-4f-4=-13 \\\ & \Rightarrow 4g+2f=-13+4 \\\ \end{aligned}$$ $$\Rightarrow 4g+2f=-9$$ Multiplying by 2 in the above equation, we get $$\Rightarrow 2\times \left( 4g+2f \right)=-9\times 2$$ $$\Rightarrow 8g+4f=-18$$ …………………(9) Now, subtracting equation (9) from equation (8), we get $$\begin{aligned} & \Rightarrow \left( 8g+6f \right)-\left( 8g+4f \right)=-37-\left( -18 \right) \\\ & \Rightarrow 8g+6f-8g-4f=-37+18 \\\ & \Rightarrow 2f=-19 \\\ \end{aligned}$$ $$\Rightarrow f=\dfrac{-19}{2}$$ …………………..(10) Now, putting the value of f from equation (10) in equation (6), we get $$\begin{aligned} & \Rightarrow c=-4-4\left( -\dfrac{19}{2} \right) \\\ & \Rightarrow c=-4+38 \\\ \end{aligned}$$ $$\Rightarrow c=34$$ ………………….(11) Now, putting the value of f from equation (10) in equation (8), we get $$\begin{aligned} & \Rightarrow 8g+6\left( \dfrac{-19}{2} \right)=-37 \\\ & \Rightarrow 8g-3\times 19=-37 \\\ & \Rightarrow 8g-57=-37 \\\ & \Rightarrow 8g=57-37 \\\ & \Rightarrow 8g=20 \\\ \end{aligned}$$ $$\Rightarrow g=\dfrac{20}{8}=\dfrac{5}{2}$$ …………………………..(12) Now, putting the value of g from equation (12), f from equation (10), and c from equation (11), in the equation of the circle $${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$$ , we get $${{x}^{2}}+{{y}^{2}}+2g\left( \dfrac{5}{2} \right)+2f\left( \dfrac{-19}{2} \right)+34=0$$ $$\Rightarrow {{x}^{2}}+{{y}^{2}}+5x-19y+34=0$$ ……………………….(13) Now, we have got the equation of the circle. Since the point D $$\left( 0,t \right)$$ is also concyclic so, the coordinate of the point D must also satisfy the equation of the circle. The equation of the circle is $${{x}^{2}}+{{y}^{2}}+5x-19y+34=0$$ . Putting the coordinate of the point D $$\left( 0,t \right)$$ in the equation of the circle, we get $$\begin{aligned} & \Rightarrow {{\left( 0 \right)}^{2}}+{{\left( t \right)}^{2}}+5\left( 0 \right)-19\left( t \right)+34=0 \\\ & \Rightarrow {{t}^{2}}-19t+34=0 \\\ & \Rightarrow {{t}^{2}}-17t-2t+34=0 \\\ & \Rightarrow t\left( t-17 \right)-2\left( t-17 \right)=0 \\\ & \Rightarrow \left( t-2 \right)\left( t-17 \right)=0 \\\ \end{aligned}$$ Here we have, $$t-2=0,t-17=0$$ . So, $$t=2$$ and $$t=17$$ . Therefore, the value of t is 2 or 17. Note: In this question, one may think that the points A, B, C, and D are lying on a common straight line. This is wrong. If a set of points lie on the same straight line, the points are said to be collinear. Here, it is given that the points are concyclic which means that points A, B, C, and D are lying on a common circle.