Question

The points $A\left( {7,3} \right)$ and $C\left( {0, - 4} \right)$ are two opposite vertices of a rhombus ABCD, find the equation of the diagonal BD.

Answer 1

Consider a point $M$ as the midpoint of diagonals $AC$ and $BD$, and find its coordinates using the midpoint line segment formula to get the required answer. Diagonals in the rhombus are perpendicular to each other. Use slope point form to get the required line equation of the diagonal BD. So, use this concept to reach the solution of the given problem.

Complete step-by-step answer :
Let $M$ be the midpoint of diagonals $AC$ and $BD$ as shown in the below figure:

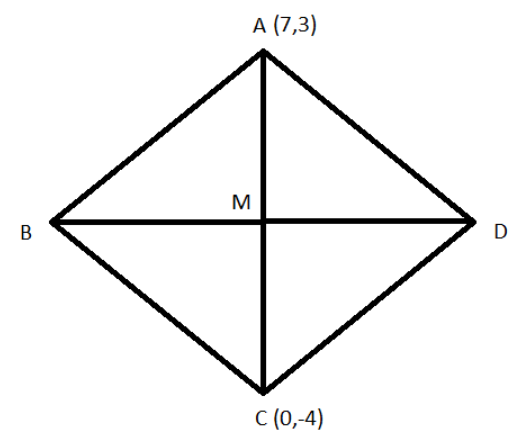
Given points are $A\left( {7,3} \right)$ and $C\left( {0, - 4} \right)$
We know that the midpoint of the points $\left( {{x_1},{y_1}} \right){\text{ and }}\left( {{x_2},{y_2}} \right)$ is given by $\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$.
Therefore, coordinates of point $M$ are:
$M\left( {\dfrac{{7 + 0}}{2},\dfrac{{3 - 4}}{2}} \right) = \left( {\dfrac{7}{2},\dfrac{{ - 1}}{2}} \right)$
As we know that in a rhombus diagonal are perpendicular to each other i.e., $BD \bot AC$
So, the slopes of BD and AC are also perpendicular.
The slope of the line joining points $\left( {{x_1},{y_1}} \right){\text{ and }}\left( {{x_2},{y_2}} \right)$ is given by $\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
So, slope of the line AC $= \dfrac{{ - 4 - 3}}{{0 - 7}} = \dfrac{{ - 7}}{{ - 7}} = 1$
Let $m$ be the slope of the line BD.
We know that the condition of perpendicularity of the two slopes ${m_1}$ and ${m_2}$ is ${m_1} \times {m_2} = - 1$.
As the slopes of BD and AC are perpendicular, we have

$$\Rightarrow m \times 1 = - 1 \\\ \therefore m = - 1 \\\$$

We know that the line equation of a line with slope $m$and is passing through a point $\left( {{x_1},{y_1}} \right)$ is given by $y - {y_1} = m\left( {x - {x_1}} \right)$. This formula is called a slope point form.
Since the point $M\left( {\dfrac{7}{2},\dfrac{{ - 1}}{2}} \right)$ is passing through the line BD with slope $- 1$, we have the line equation as

$$\Rightarrow y - \left( {\dfrac{{ - 1}}{2}} \right) = - 1\left( {x - \dfrac{7}{2}} \right) \\\ \Rightarrow y + \dfrac{1}{2} = - x + \dfrac{7}{2} \\\ \Rightarrow x + y = \dfrac{7}{2} - \dfrac{1}{2} = \dfrac{6}{2} = 3 \\\ \therefore x + y = 3 \\\$$

Note : The midpoint of the points $\left( {{x_1},{y_1}} \right){\text{ and }}\left( {{x_2},{y_2}} \right)$ is given by $\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$. The line equation of a line with slope $m$and is passing through a point $\left( {{x_1},{y_1}} \right)$ is given by $y - {y_1} = m\left( {x - {x_1}} \right)$. This formula is called a slope point form.