Question

The points $A\left( {1,3} \right)\& C\left( {5,1} \right)$ are two opposite vertices of a rectangle. The other two vertices of a rectangle lie on the line $y = 2x + c$. Find $c$ & the remaining vertices.
A. $c = 4;B\left( {2,0} \right);D\left( {4,4} \right)$
B. $c = - 4;B\left( {2,0} \right);D\left( {4,4} \right)$
C. $c = - 4;B\left( { - 2,0} \right);D\left( { - 4,2} \right)$
D. $c = 4;B\left( {2,0} \right);D\left( { - 4, - 4} \right)$

Answer 1

We are asked to find out the intercept and the vertices of the other diagonal. So, using the vertices given we can find out the midpoint of that particular diagonal. Then using the property that the diagonal of a rectangle bisects each other and has the same midpoint, we can find out the intercept as the mid-point lies on the line given $y = 2x + c$ and then proceed further.

Complete step-by-step answer:
Let $A\left( {1,3} \right),B\left( {{x_1},{y_1}} \right),C\left( {5,1} \right)\& D\left( {{x_2},{y_2}} \right)$ be the vertices of the rectangular as shown in the given below figure:

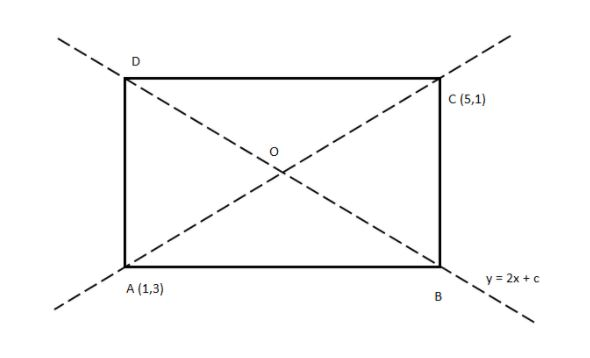
Let O be the point of intersection of diagonal AC and BD.
Therefore, Midpoint of AC = Midpoint BD.
Midpoint of AC = O $= \left( {\dfrac{{1 + 5}}{2},\dfrac{{3 + 1}}{2}} \right) = \left( {3,2} \right)$
Since, ${\text{O}}\left( {3,2} \right)$ lies on $y = 2x + c$ we have

$$\Rightarrow 2 = 2 \times 3 + c \\\ \therefore c = 2 - 6 = - 4 \\\$$

Thus, the line becomes $y = 2x - 4$
Also, $\left( {{x_1},{y_1}} \right)$ lies on the line $y = 2x - 4$.
$\Rightarrow {y_1} = 2{x_1} - 4.....................\left( 1 \right)$
Also, $\left( {{x_2},{y_2}} \right)$ lies on $y = 2x - 4$
$\Rightarrow {y_2} = 2{x_2} - 4...................................\left( 2 \right)$
So, Coordinates of B $= \left( {{x_1},2{x_1} - 4} \right){\text{ }}\left[ {\because {\text{equation }}\left( 1 \right)} \right]$
And Coordinates of D $= \left( {{x_2},2{x_2} - 4} \right){\text{ }}\left[ {\because {\text{equation }}\left( 2 \right)} \right]$
Since $ABCD$ is a rectangle, we have $AD \bot AB$
Therefore, slope of AB × slope of BC $= - 1$
We know that slope of two points $P\left( {a,b} \right)\& Q\left( {c,d} \right)$ is given by $\dfrac{{d - c}}{{b - a}}$

$$\Rightarrow \left( {\dfrac{{2x - 4 - 3}}{{x - 1}}} \right) \times \left( {\dfrac{{2x - 4 - 1}}{{x - 5}}} \right) = - 1 \\\ \Rightarrow \left( {2x - 7} \right)\left( {2x - 5} \right) = - \left( {x - 1} \right)\left( {x - 5} \right) \\\$$

Multiplying the terms inside the brackets, we have

$$\Rightarrow 4{x^2} - 24x + 35 = - {x^2} - 5 + 6x \\\ \Rightarrow 5{x^2} - 30x + 40 = 0 \\\$$

Dividing with 5 on both sides, we have

$$\Rightarrow {x^2} - 6x + 8 = 0 \\\ \Rightarrow {x^2} - 2x - 4x + 8 = 0 \\\ \Rightarrow \left( {x - 2} \right)\left( {x - 4} \right) = 0 \\\ \therefore {x_1} = 2\& {x_2} = 4 \\\$$

Substituting ${x_1} = 2$, in coordinates of B we get
Coordinates of B $= \left( {2,2 \times 2 - 4} \right) = \left( {2,0} \right)$
Substituting ${x_2} = 4$, in coordinates of D we get
Coordinates of D $= \left( {4,2 \times 4 - 4} \right) = \left( {4,4} \right)$
Thus, the other two vertices of the rectangle are $B\left( {2,0} \right);D\left( {4,4} \right)$

So, the correct answer is “Option B”.

Note: For such questions, you must know the properties of rectangle and point lying on a plane. You must know how to find the slope of a line and be able to differentiate what is the slope in the equation of a line and what is intercept.