Question

The points ( 7, 2 ) and ( -1, 0 ) lie on a line $\ldots \ldots$

A) $7y = 3x - 7$

B) $4y = x + 1$

C) $y = 7x + 7$

D) $x = 4y + 1$

Answer 1

We have given two points and we need to find a line where these two points lie. This line equation will be the same as the line joining these two points.

We will use the two point form of the straight line and find the required answer.

**
**

Formula used:

If $(x_1,y_1)$ and $(x_2,y_2)$ are two points, then the line joining these two points is given by the two point form as

$y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right)$

Complete step by step answer:

Given, ( 7, 2 ), ( -1 ,0 ) are the two points

Two point form of a line if two points are $\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right)$ is

$y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right)$ using this formula or form of line we will write equation of line.

Here in this question,

$\left( {{x_1} = 7,{y_1} = 2} \right),\left( {{x_2} = - 1,{y_2} = 0} \right)$

On substituting the corresponding values in the two point form formula,

$y - 2 = \dfrac{{0 - 2}}{{ - 1 - 7}}\left( {x - 7} \right)$

On simplification,

$y - 2 = \dfrac{{ - 2}}{{ - 8}}\left( {x - 7} \right)$

$\Rightarrow y - 2 = \dfrac{1}{4}\left( {x - 7} \right)$

$4y - 8 = x - 7$

On rearranging we get,

$4y = x +1$

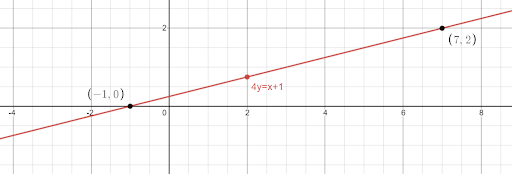
This is the required line equation where the points ( 7, 2 ) and ( -1, 0 ) lie.

Hence option (B) is the correct option.

Note: Whenever we get this type of question the key concept of solving is we can write an equation of line using two points. And here one thing is important. If this type of question comes in an exam you have no need of writing an equation just put the points in the option and check which option is satisfying that will be answered.

We can see the graph of the line $4y = x +1$ along with the points ( 7, 2 ) and ( -1, 0 ) below.