Solveeit Logo
Login

Question

Question: The points (−2, 1), (0, 3), (2, 1) and (0, −1) are the vertices of a ____. A) Parallelogram B) S...

The points (−2, 1), (0, 3), (2, 1) and (0, −1) are the vertices of a ____.
A) Parallelogram
B) Scalene quadrilateral
C) Isosceles quadrilateral
D) Concave quadrilateral

Explanation

Solution

Hint: For solving this question, we use the concept that if the points are P(x1,y1)P\left( {{x}_{1}},{{y}_{1}} \right) and Q(x2, y2),Q\left( {{x}_{2}},\text{ }{{y}_{2}} \right), then the slope of the line joining PQ is y2−y1x2−x1\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}. Four different points are given in the question. Using these points, we calculate slopes of 4 lines. Using these slopes, we can easily determine the shape of the figure.
Complete step-by-step answer:
If the points are P(x1,y1)P\left( {{x}_{1}},{{y}_{1}} \right) and Q(x2, y2),Q\left( {{x}_{2}},\text{ }{{y}_{2}} \right), the slope of the line joining PQ is y2−y1x2−x1\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}.
Points given in the questions are A (-2, 1), B (0, 3), C (2, 1) and D (0, -1).
Now, slope of the line AB joining points A (-2, 1) and B (0, 3) is:
=3−10−(−2) =20+2 =1 \begin{aligned} & =\dfrac{3-1}{0-\left( -2 \right)} \\\ & =\dfrac{2}{0+2} \\\ & =1 \\\ \end{aligned}
Slope of line AB =1.=1.
Slope of the line BC joining points B (0, 3) and C (2, 1) is:
=1−32−0 =−22 =−1 \begin{aligned} & =\dfrac{1-3}{2-0} \\\ & =\dfrac{-2}{2} \\\ & =-1 \\\ \end{aligned}
Slope of line AB =−1.=-1.
slope of the line CD joining points C (2, 1) and D (0, -1) is:
=−1−10−2 =−2−2 =1 \begin{aligned} & =\dfrac{-1-1}{0-2} \\\ & =\dfrac{-2}{-2} \\\ & =1 \\\ \end{aligned}
Slope of line CD =1.=1.
Slope of the line DA joining points D (0, -1) and A (-2, 1) is:
=−1−10−(−2) =−20+2 =−1 \begin{aligned} & =\dfrac{-1-1}{0-\left( -2 \right)} \\\ & =\dfrac{-2}{0+2} \\\ & =-1 \\\ \end{aligned}
Slope of line DA =−1.=-1.
As we can see that the slopes of AB and CD are the same. Therefore, AB||CD.
Similarly, the slope of BC and slope of DA are also the same. Therefore, BC||DA.
Since, the opposite sides are parallel to each other.
Hence, A, B, C and D are the vertices of the parallelogram.
Therefore, option (a) is correct.

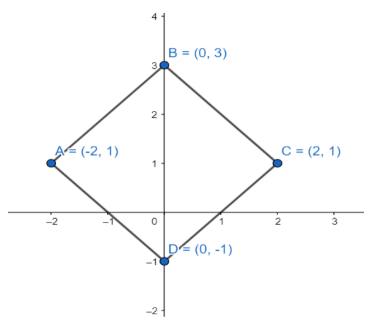
Note: Students can also solve this problem by constructing a proper figure using the cartesian system of coordinates as shown above. Once the figure ABCD is obtained, we can easily predict that the figure is rhombus which is a special form of parallelogram.