Question

The point represented by $2 + i$ in the argand plane moves 1 unit eastwards, then 2 units northwards and finally from there $2\sqrt 2$units in the south-westwards direction. Then its new position in the argand plane is at the point represented by:
A. -1-i
B. 2+2i
C. 1+i
D. -2-2i

Answer 1

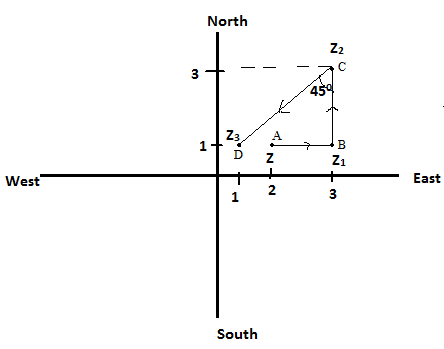
In this question, we will move step by step. First move is toward the right. So, the real part of Z will get incremented. After this next move is towards the north, so the imaginary part now gets incremented. Finally we find the component of the south-east move to get the final location point.

Complete step-by-step answer:
Let the initial point be at A whose value is Z = 2+i
Now, point moves one unit eastward which means there will be increment in the real part of complex number Z.
$\therefore$ New position will be at B given by ${Z_1}$ = (2+1) +i = 3+i
And again the point moves 2 units northwards which means there will be an increment in the imaginary part of complex number${Z_1}$.
$\therefore$ New position will be at C given by${Z_2}$ = 3 + (2+1) i= 3+3i.
And finally it moves $2\sqrt 2$ unit in the south-westwards direction. If we divide this move in vertical and horizontal component, then
Movement in south direction = $2\sqrt 2 \operatorname{Cos} {45^0} = 2\sqrt 2 \times \dfrac{1}{{\sqrt 2 }} = 2$.
Movement in west direction = $2\sqrt 2 \operatorname{Sin} {45^0} = 2\sqrt 2 \times \dfrac{1}{{\sqrt 2 }} = 2$ .
If we take north and east as positive then west and south move will be negative.
And the final position will be at D given by ${Z_3}$ = (3-2)+(3-2)i = 1+i.

Therefore, option C is correct.

So, the correct answer is “Option A”.

Note: Whenever we come to these types of problems always draw a figure with notify direction and remember east-west direction shows real part of complex number and north-south direction shows imaginary part of complex number.