Solveeit Logo
Login

Question

Question: The point P on the parabola \({{y}^{2}}=4ax\) for which \(\left| PR-PQ \right|\) is maximum, where \...

The point P on the parabola y2=4ax{{y}^{2}}=4ax for which ∣PR−PQ∣\left| PR-PQ \right| is maximum, where R(−a, 0)R\left( -a,\text{ }0 \right) and Q (0, a)Q\text{ }\left( 0,\text{ }a \right) is,
A. (a,2a)\left( a,2a \right)
B. (a,−2a)\left( a,-2a \right)
C. (4a,4a)\left( 4a,4a \right)
D. (4a,−4a)\left( 4a,-4a \right)

Explanation

Solution

Firstly, draw a diagram to represent the coordinates and the parabola and then decide which length will be denoting the maximum length of ∣PR−PQ∣\left| PR-PQ \right| . This is possible when PQR is a line. Now equate the slopes of PQ and PR. Use the general denotation for any point on the parabola and then find the coordinate of P.

Complete step-by-step solution:
The given equation of the parabola is y2=4ax{{y}^{2}}=4ax
Let P be any point on the parabola.
Any point on a parabola is generally denoted by the coordinates,
P(at2,2at)P\left( a{{t}^{2}},2at \right)
Its diagrammatic representation is given by,

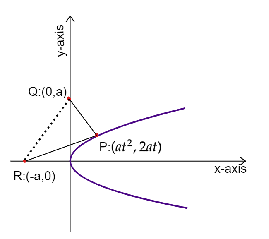
When we look at the triangle PQR,
We can say that always,
⇒∣PR−PQ∣≤QR\Rightarrow \left| PR-PQ \right|\le QR
Hence the maximum value of ∣PR−PQ∣\left| PR-PQ \right| will be QR.
The maximum value of ∣PR−PQ∣\left| PR-PQ \right| is QR and is achieved when PQR is a straight line.
And for PQR to be a straight line,
The slope of PR must be equal to the slope of PQ.
Now let us write the slope form for the above condition.
We know that P(at2,2at)P\left( a{{t}^{2}},2at \right) ,
And R(−a, 0)R\left( -a,\text{ }0 \right) and Q (0, a)Q\text{ }\left( 0,\text{ }a \right)
Upon substituting in slope equations, we get,
⇒(2at−0at2+a)=(2at−aat2−0)\Rightarrow \left( \dfrac{2at-0}{a{{t}^{2}}+a} \right)=\left( \dfrac{2at-a}{a{{t}^{2}}-0} \right)
Now evaluate to find the value of t from the expression.
⇒(2atat2+a)=(2at−aat2)\Rightarrow \left( \dfrac{2at}{a{{t}^{2}}+a} \right)=\left( \dfrac{2at-a}{a{{t}^{2}}} \right)
Cancel ‘a’ from both sides as it is common on the numerator and denominator.
⇒(2tt2+1)=(2t−1t2)\Rightarrow \left( \dfrac{2t}{{{t}^{2}}+1} \right)=\left( \dfrac{2t-1}{{{t}^{2}}} \right)
Now cross multiply the expressions.
⇒2t×t2=(t2+1)(2t−1)\Rightarrow 2t\times {{t}^{2}}=\left( {{t}^{2}}+1 \right)\left( 2t-1 \right)
Evaluate further.
⇒2t3=2t3−t2+2t−1\Rightarrow 2{{t}^{3}}=2{{t}^{3}}-{{t}^{2}}+2t-1
Now, cancel the common terms on both sides of the expression.
⇒t2−2t+1=0\Rightarrow {{t}^{2}}-2t+1=0
⇒(t−1)2=0\Rightarrow {{\left( t-1 \right)}^{2}}=0
Which upon solving gives us t=1t=1
Now substitute this in the general coordinates of P(at2,2at)P\left( a{{t}^{2}},2at \right) ,
We get,
⇒P(a(1)2,2a(1))\Rightarrow P\left( a{{\left( 1 \right)}^{2}},2a\left( 1 \right) \right)
⇒P(a,2a)\Rightarrow P\left( a,2a \right)
Hence option A is correct.

Note: The slope of a line is the steepness of a line in a horizontal or vertical direction. The slope of a line can be calculated by taking the ratio of the change in vertical dimensions upon the change in horizontal dimensions.