Question

The point $P(a,b)$ lies on the straight line $3x + 2y = 13$ and the point $Q(b,a)$ lies on the straight line $4x - y = 5$, then the equation of line $PQ$ is

1. $x - y = 5$
2. $x + y = 5$
3. $x + y = - 5$
4. $x - y = - 5$

Answer 1

Hint : In this question we have to find the line equation of $PQ$. These two points, $P$ and $Q$ lie on a straight line. So let substitute the points values in the corresponding line equations to know the value of points. After finding those values, substitute it in the line equation to get the equation of line $PQ$.
Formula used:
Equation of line passing through two points $({x_1},{y_1}),({x_2},{y_2})$ is $\dfrac{{y - {y_1}}}{{{y_2} - {y_1}}} = \dfrac{{x - {x_1}}}{{{x_2} - {x_1}}}$.

Complete step-by-step answer :
We are going to draw a graph for the given problem.

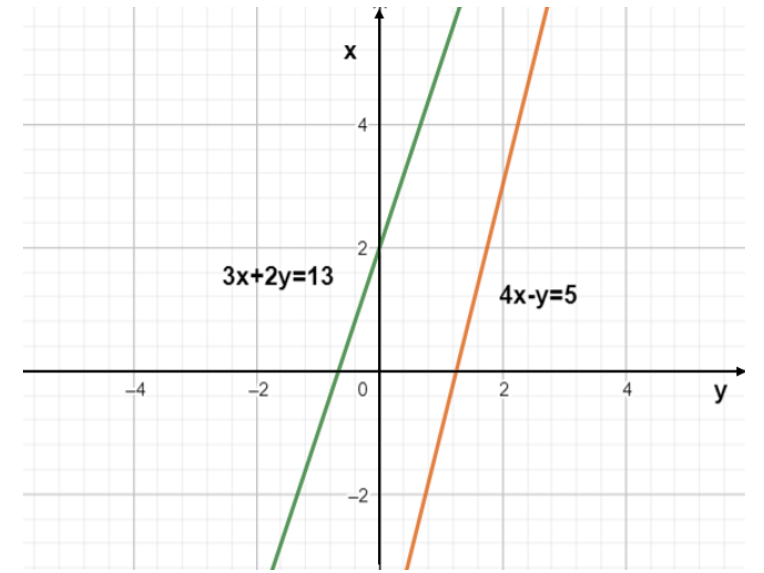
The Point $P(a,b)$ lies on the straight line $3x + 2y = 13$.
So substitute $(a,b)$ in the place of $(x,y)$. That is $x = a$ and $y = b$.
Then, $3a + 2b = 13$ ……………………………. ($1$)
Point $Q(b,a)$ lies on the straight line $4x - y = 5$, substitute as $x = b$ and $y = a$.
$4b - a = 5$ , this can be rewrite as $- a + 4b = 5$ …………………………………………. ($2$)
Multiply equation $2$ by $3 \Rightarrow - 3a + 12b = 15$ ……………………………. ($3$)
Add equation $1$ and $3$,

$$\underline 3a + 2b = 13 \\\ \- 3a + 12b = {15_{( + )}} \\\ \\\ {\text{ }}0 + 14b = 28 \\\$$

We will get $14b = 28$,
Then, $b = \dfrac{{28}}{{14}} = 2$
Therefore we get $b = 2$, and substitute this equation to get the value of $a$.
Here, substitute $b = 2$ in equation $1$,
$3a + 2(2) = 13$
$3a + 4 = 13$
Keeping variable and numerals in separate sides,
$a = \dfrac{{13 - 4}}{3}$
$a = \dfrac{9}{3}$
We will get, $a = 3$.
Finally we have found $a = 3$ and $b = 2$. Now substitute in the equation of the line passing through two points.
Point $P(3,2)$ and $Q(2,3)$. In point $PQ$ ${x_1} = 3,{y_1} = 2$ and ${x_2} = 2,{y_2} = 3$.
Equation of line passing through two points $(3,2),(2,3)$ is $\dfrac{{y - 2}}{{3 - 2}} = \dfrac{{x - 3}}{{2 - 3}}$
By solving this, we will get
$\dfrac{{y - 2}}{1} = \dfrac{{x - 3}}{{ - 1}}$
Place the $-$ sign in the denominator in numerator,
$\dfrac{{y - 2}}{1} = \dfrac{{ - (x - 3)}}{1}$
Here the denominators are $1$, any number divided by $1$ is the number itself. So it can be written as $y - 2 = - (x - 3)$.
Multiply $-$ sign inside the bracket,
$y - 2 = - x + 3$
Write the variables in L.H.S. and numerals in R.H.S.,
$x + y = 3 + 2$
$x + y = 5$.
Therefore the equation of line $PQ$ is $x + y = 5$.
Hence option (2) is correct.

Note : There are many methods to find the value of variables. Here, the values of $a$ and $b$ are found by applying the elimination method in two equations. It can also be found by the substitution method. By substituting the value of one variable from one equation in another equation. However the final result will be the same only.