Question

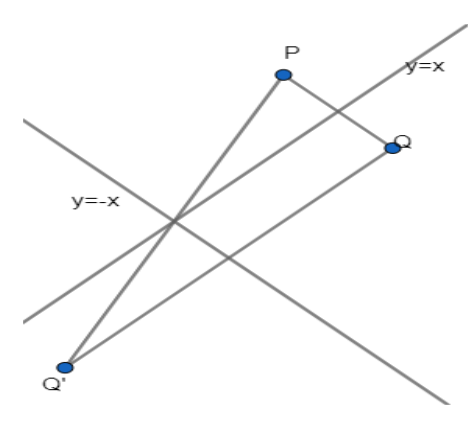
The point P(3,6) is first reflected on the line $y=x$ and then the image point Q is again reflected on the line $y=-x$ to get the image point Q'. Then the circumcentre of the $\Delta PQQ'$ is.
(a) (6,3)
(b) (6,-3)
(c) (3,-6)
(d) (0,0)

Answer 1

Hint: In this question, by using the given conditions we need to find the coordinates of the vertices. Then find the equations of any two bisectors by using the point slope formula. The intersection of these two bisectors will be the circumcentre.

Complete step-by-step solution -
Circumcentre of a triangle is the point of intersection of the bisectors.
Bisector of a side is perpendicular to that side and passes through the midpoint of that side.
Now, on reflecting the point P(3,6) about the line $y=x$ then the coordinates of the points get interchanged which gives.
$Q=\left( 6,3 \right)$
Now, again on reflecting this point about the line $y=-x$ then the coordinates of the points get interchanged and so the signs which give.
$Q'=\left( -3,-6 \right)$

As we already know that slope of a line joining two points $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ is given by
$m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
The midpoint of the points $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$is given by
$\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
The equation of the line with slope m and passing through the point $\left( {{x}_{1}},{{y}_{1}} \right)$ is given by
$y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$
Now, to find the bisector of the side PQ' we need to find its midpoint and its slope.
Now, on comparing with the above formulae we get,
${{x}_{1}}=3,{{x}_{2}}=-3,{{y}_{1}}=6,{{y}_{2}}=-6$
Midpoint of PQ' is given by

& \Rightarrow \left( \dfrac{3-3}{2},\dfrac{6-6}{2} \right) \\\ & \Rightarrow \left( 0,0 \right) \\\ \end{aligned}$$ Slope of PQ' is given by $$\begin{aligned} & \Rightarrow m=\dfrac{-6-6}{-3-3} \\\ & \Rightarrow m=\dfrac{-12}{-2} \\\ & \therefore m=2 \\\ \end{aligned}$$ Now, as the bisector will be perpendicular to PQ' we get, $$\begin{aligned} & \Rightarrow m'\times m=-1 \\\ & \Rightarrow m'\times 2=-1 \\\ & \therefore m'=\dfrac{-1}{2} \\\ \end{aligned}$$ Now, on substituting the respective values in the point slope formula we get the equation of the bisector of PQ' as $$\Rightarrow y-0=\dfrac{-1}{2}\left( x-0 \right)$$ Now, on cross multiplying and rearranging the terms we get, $$\Rightarrow x+2y=0.......\left( 1 \right)$$ Now, to find the bisector of the side PQ we need to find its midpoint and its slope. Now, on comparing with the above formulae we get, $${{x}_{1}}=3,{{x}_{2}}=6,{{y}_{1}}=6,{{y}_{2}}=3$$ Midpoint of PQ is given by $$\begin{aligned} & \Rightarrow \left( \dfrac{3+6}{2},\dfrac{6+3}{2} \right) \\\ & \Rightarrow \left( \dfrac{9}{2},\dfrac{9}{2} \right) \\\ \end{aligned}$$ Slope of PQ is given by $$\begin{aligned} & \Rightarrow m=\dfrac{3-6}{6-3} \\\ & \Rightarrow m=\dfrac{-3}{3} \\\ & \therefore m=-1 \\\ \end{aligned}$$ Now, as the bisector will be perpendicular to PQ we get, $$\begin{aligned} & \Rightarrow m'\times m=-1 \\\ & \Rightarrow m'\times -1=-1 \\\ & \therefore m'=1 \\\ \end{aligned}$$ Now, on substituting the respective values in the point slope formula we get the equation of the bisector of PQ as $$\Rightarrow y-\dfrac{9}{2}=1\left( x-\dfrac{9}{2} \right)$$ Now, on cross multiplying and rearranging the terms we get, $$\Rightarrow x-y=0....\left( 2 \right)$$ Now, by solving the equations (1) and (2) we get the circumcentre. $$\begin{aligned} & \Rightarrow x-y=0 \\\ & \Rightarrow x+2y=0 \\\ \end{aligned}$$ $$\therefore x=0,y=0$$ Hence, the circumcentre of the triangle is (0,0) option (d). Note: Instead of finding the bisectors of the sides and then finding their point of intersection we can also find it by assuming some variable coordinates and then considering the condition that circumcentre is equidistant from all the vertices by using the distance and solving we get the result. But, this will be a little lengthy. While calculating the bisector equation, slope and midpoint there should not be any calculation mistakes or neglecting the terms. It is also to be noted that slope of the bisector is not the slope obtained by the slope joining the two points. It is perpendicular to the slope obtained by the formula of slope joining the two points.