Question
Question: The point on the curve \[{{y}^{2}}=x\], where tangent makes \[{{45}^{\circ }}\] angle with x-axis is...
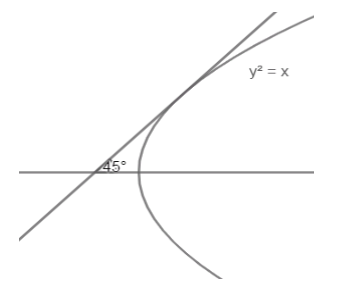
The point on the curve y2=x, where tangent makes 45∘ angle with x-axis is
(a) (21,41)
(b) (41,21)
(c) (4,2)
(d) (1,1)
Solution
Hint: In this question, from the given value of angle made by the tangent with x-axis we get the slope of the tangent. Then using the formula of tangent to parabola y2=4ax at point (x1,y1) given by yy1=2a(x+x1) we get the equation of tangent for the given parabola. Now, on equating the slope to 1 from the equation we get the coordinates.
Complete step-by-step answer:
Let us assume the point on the parabola as (x1,y1)
Now, on comparing the given equation of parabola y2=x with the standard form y2=4ax we get,
⇒4a=1
Now, on dividing both sides with 4 we get,
⇒a=41
Equation of Tangent:
The equation of the tangent to the parabola y2=4ax at a point (x1,y1) is given by
⇒yy1=2a(x+x1)
Now, from the given parabola y2=x the equation of tangent (x1,y1) is given by
⇒yy1=2a(x+x1)
Now, on substituting the respective values we get,
⇒yy1=42(x+x1)
Now, on further simplification this can also be written as
⇒yy1=21(x+x1)
Let us now multiply with two on both sides
⇒2yy1=x+x1
Now, on rearranging the terms we get,
⇒x−2yy1+x1=0
As we already know that slope of a line ax+by+c=0 is given by
m=a−b
Let us assume the slope of the tangent as m
Now, on comparing this with the equation of tangent we get,
a=1,b=−2y1
Now, on substituting these values in the slope formula we get,
⇒m=1−(−2y1)
Now, on further simplification we get,
⇒m=2y1
Now, given in the question that the tangent makes 45∘with the x-axis
As we already know that tangent of the angle made by the line with x-axis gives its slope
Now, from the above condition we get,
⇒m=tan45∘
Now, this can be written as
⇒m=1
Let us now substitute the value of m obtained above
⇒2y1=1
Now, on dividing both sides with 2 we get,
∴y1=21
As this point lies on the curve y2=xwe have the condition
⇒y12=x1
Now, on substituting the respective value we get,
⇒x1=(21)2
Now, on further simplification we get,
∴x1=41
∴(x1,y1)=(41,21)
Hence, the correct option is (b).
Note:Instead of writing the equation of tangent in point form we can directly write in the slope form and then substitute the value of slope from a given angle made with x-axis. Now, on further simplification we get the result. Both the methods give the same result.
It is important to note that we need to equate the slope from the equation with the slope obtained from the angle made by tangent with the x-axis. It is also to be noted that to get the value of x coordinate we need to substitute it in the curve equation given as the point lies on it.
