Question

The point of the parabola ${{y}^{2}}=64x$ which is nearest to the line $4x+3y+35=0$ has coordinates

1. $\left( 9,-24 \right)$
2. $\left( 1,81 \right)$
3. $\left( 4,-16 \right)$
4. $\left( -9,-24 \right)$

Answer 1

In this type of question we have to use a distance formula. We know that the distance of the point $\left( {{x}_{0}},{{y}_{0}} \right)$ from the line $ax+by+c=0$ is given by, $d=\dfrac{\left| a{{x}_{0}}+b{{y}_{0}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$. Also we know that if its derivative is equal to zero then the distance is minimum.

Complete step-by-step solution:
Now we have to find the coordinates of the point on the parabola ${{y}^{2}}=64x$ which is nearest to the line $4x+3y+35=0$

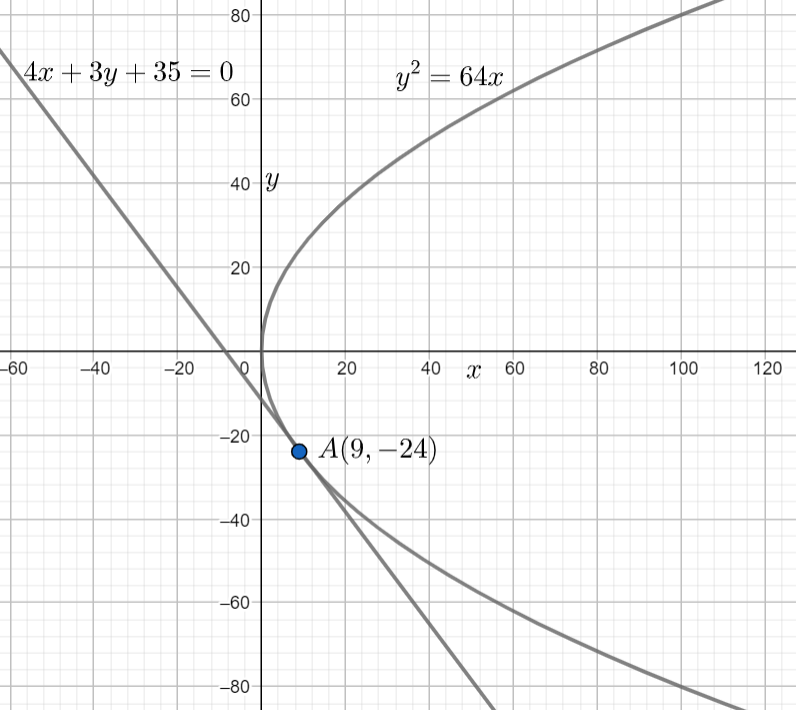
Let us suppose that the point $P\left( {{x}_{0}},{{y}_{0}} \right)$ is point on the parabola nearest to the line $4x+3y+35=0$.
Now, as the point $P\left( {{x}_{0}},{{y}_{0}} \right)$ is on the parabola ${{y}^{2}}=64x$
$\Rightarrow {{y}_{0}}^{2}=64{{x}_{0}}\cdots \cdots \cdots \left( i \right)$
As we know that the distance of the point $\left( {{x}_{0}},{{y}_{0}} \right)$ from the line $ax+by+c=0$ is given by, $d=\dfrac{\left| a{{x}_{0}}+b{{y}_{0}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$.
Hence, the distance of the point $P\left( {{x}_{0}},{{y}_{0}} \right)$ from the line $4x+3y+35=0$ is

& \Rightarrow d=\dfrac{\left| 4{{x}_{0}}+3{{y}_{0}}+35 \right|}{\sqrt{{{4}^{2}}+{{3}^{2}}}} \\\ & \Rightarrow d=\dfrac{\left| 4{{x}_{0}}+3{{y}_{0}}+35 \right|}{\sqrt{25}} \\\ & \Rightarrow d=\dfrac{\left| 4{{x}_{0}}+3{{y}_{0}}+35 \right|}{5} \\\ \end{aligned}$$ $$\Rightarrow d=\dfrac{4}{5}{{x}_{0}}+\dfrac{3}{5}{{y}_{0}}+7$$ Now by using equation $$\left( i \right)$$ we will get $${{x}_{0}}=\dfrac{{{y}_{0}}^{2}}{64}$$ and hence we can write $$\begin{aligned} & \Rightarrow d=\dfrac{4}{5}\left( \dfrac{{{y}_{0}}^{2}}{64} \right)+\dfrac{3}{5}{{y}_{0}}+7 \\\ & \Rightarrow d=\dfrac{{{y}_{0}}^{2}}{80}+\dfrac{3}{5}{{y}_{0}}+7 \\\ \end{aligned}$$ Now as we have to find the nearest point, we have to minimise the distance and for that we differentiate the distance with respect to $${{y}_{0}}$$ and equate it to zero $$\begin{aligned} & \Rightarrow \dfrac{d}{d{{y}_{0}}}\left( d \right)=0 \\\ & \Rightarrow \dfrac{d}{d{{y}_{0}}}\left( \dfrac{{{y}_{0}}^{2}}{80}+\dfrac{3}{5}{{y}_{0}}+7 \right)=0 \\\ & \Rightarrow \dfrac{2{{y}_{0}}}{80}+\dfrac{3}{5}=0 \\\ & \Rightarrow \dfrac{{{y}_{0}}}{40}=-\dfrac{3}{5} \\\ & \Rightarrow {{y}_{0}}=-24 \\\ \end{aligned}$$ Now we substitute this value of $${{y}_{0}}$$ in equation $$\left( i \right)$$ we get, $$\begin{aligned} & \Rightarrow {{x}_{0}}=\dfrac{{{y}_{0}}^{2}}{64} \\\ & \Rightarrow {{x}_{0}}=\dfrac{{{\left( -24 \right)}^{2}}}{64} \\\ & \Rightarrow {{x}_{0}}=9 \\\ \end{aligned}$$ So, the coordinates of the point is $$\left( 9,-24 \right)$$ **Thus, option (1) is the correct option.** **Note:** In this type of question students have to remember the formula of finding the distance of a point from the line. Students have to note that they can find the minimum distance with the help of the derivatives. Also students have to take care during the calculations.