Question
Question: The point of intersection of the lines <img src="https://cdn.pureessence.tech/canvas_631.png?top_lef...
The point of intersection of the lines  −36x+3=2y−3=4z−6 is
−36x+3=2y−3=4z−6 is
A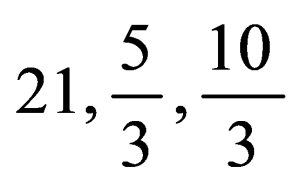
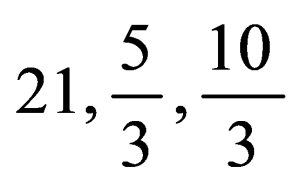
B
(2,10,4)
C
(−3,3,6)
D
(5,7,−2)
Answer
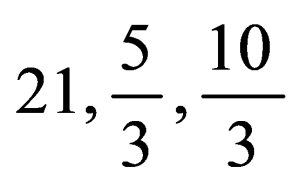
Explanation
Solution
Given lines are, 3x−5=−1y−7=1z+2=r1, (say)
and −36x+3=2y−3=4z−6=r2 , (say)
∴ x=3r1+5=−36r2−3, y=−r1+7=3+2r2 and
z=r1−2=4r2+6
On solving, we get x=21,y=35,z=310 .
Trick: Check through options.
