Solveeit Logo
Login

Question

Question: The point of intersection of the line \(\dfrac{x-1}{3}=\dfrac{y+2}{4}=\dfrac{z-3}{-2}\) and the plan...

The point of intersection of the line x−13=y+24=z−3−2\dfrac{x-1}{3}=\dfrac{y+2}{4}=\dfrac{z-3}{-2} and the plane 2x−y+3z−1=02x-y+3z-1=0 is
[a] (10,-10,3)
[b] (10,10,-3)
[c] (-10,10,3)
[d] None of these.

Explanation

Solution

Hint: Assume for the point of intersection, we have x−13=y+24=z−3−2=k\dfrac{x-1}{3}=\dfrac{y+2}{4}=\dfrac{z-3}{-2}=k. Hence find the coordinates of the point of intersection in terms of k. Since the point also lies on the plane, it must satisfy its equation. Hence form an equation in k. Solve for k and hence find the coordinates of the point of intersection. Verify your answer.

Complete step by step solution:

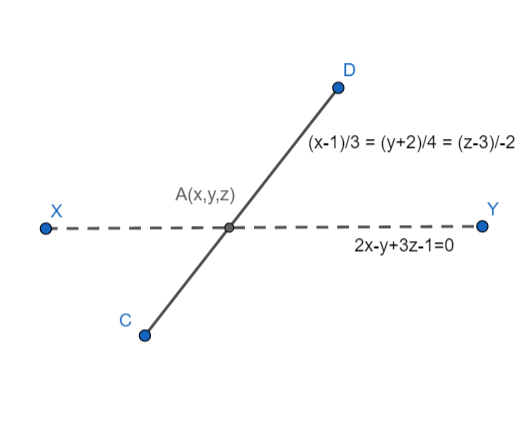
The dashed line is the sideways view of the plane 2x-y+3z-1=0 and the line CD represents the line x−13=y+24=z−3−2\dfrac{x-1}{3}=\dfrac{y+2}{4}=\dfrac{z-3}{-2}
Let A(x,y,z)A\left( x,y,z \right)be the point of intersection of the line and the plane.
Since A lies on the line x−13=y+24=z−3−2\dfrac{x-1}{3}=\dfrac{y+2}{4}=\dfrac{z-3}{-2}, we have
x−13=y+24=z−3−2=k(say)\dfrac{x-1}{3}=\dfrac{y+2}{4}=\dfrac{z-3}{-2}=k\left( say \right)
Hence, we have
x−13=k\dfrac{x-1}{3}=k
Multiplying both sides by 3, we get
x-1 =3k
Adding 1 on both sides, we get
x=3k+1x=3k+1
Also, we have
y+24=k\dfrac{y+2}{4}=k
Multiplying both sides by 4, we get
y+2=4ky+2=4k
Subtracting 2 from both sides, we get
y=4k−2y=4k-2
Also, we have
z−3−2=k\dfrac{z-3}{-2}=k
Multiplying by -2 on both sides, we get
z−3=−2kz-3=-2k
Adding 3 on both sides, we get
z=−2k+3z=-2k+3
Hence, we have
A≡(3k+1,4k−2,−2k+3)A\equiv \left( 3k+1,4k-2,-2k+3 \right)
Since A lies on the plane 2x-y+3z-1=0, A must satisfy the equation. Hence, we have
2(3k+1)−(4k−2)+3(−2k+3)−1=02\left( 3k+1 \right)-\left( 4k-2 \right)+3\left( -2k+3 \right)-1=0
Simplifying, we get
6k+2−4k+2−6k+9−1=0 ⇒−4k+12=0 \begin{aligned} & 6k+2-4k+2-6k+9-1=0 \\\ & \Rightarrow -4k+12=0 \\\ \end{aligned}
Adding 4k on both sides, we get
4k=124k=12
Dividing both sides by 4, we get
k=3k=3
Hence, we have
A≡(3(3)+1,4(3)−2,−2(3)+3)=(10,10,−3)A\equiv \left( 3\left( 3 \right)+1,4\left( 3 \right)-2,-2\left( 3 \right)+3 \right)=\left( 10,10,-3 \right)
Hence option [b] is correct.
Note: Verification:
We can verify the correctness of our solution by verifying that the point lies on both the line and the plane. In other words, we will verify that both the equations of the line and the plane are satisfied by the point.
We have
For point A
x = 10, y = 10 and z = -3
Hence, we have
x−13=10−13=3\dfrac{x-1}{3}=\dfrac{10-1}{3}=3
Also, we have
y+24=10+24=3\dfrac{y+2}{4}=\dfrac{10+2}{4}=3
Also, we have
z−3−2=−3−3−2=3\dfrac{z-3}{-2}=\dfrac{-3-3}{-2}=3
Hence, we have
x−13=y+24=z−3−2\dfrac{x-1}{3}=\dfrac{y+2}{4}=\dfrac{z-3}{-2}
Hence point A lies on the line x−13=y+24=z−3−2\dfrac{x-1}{3}=\dfrac{y+2}{4}=\dfrac{z-3}{-2}
Also, we have
2x−y+3z−1=2(10)−10+3(−3)−1=02x-y+3z-1=2\left( 10 \right)-10+3(-3)-1=0
Hence point A lies on the plane 2x−y+3z−1=02x-y+3z-1=0
Hence our answer is verified to be correct.