Question

The point of inflection of ${{\left( x-5 \right)}^{55}}{{\left( x-6 \right)}^{66}}$ is
A. 0
B. 5
C. 6
D. $\dfrac{660}{121}$

Answer 1

We first explain the process of points of inflection. We find the concept of inflection being similar to finding extremum points. The second derivative of the function gives us the solution of the problem.

Complete step by step solution:
We have to find the inflection points for $f\left( x \right)={{\left( x-5 \right)}^{55}}{{\left( x-6 \right)}^{66}}$. Inflection points are points where the function changes concavity, from being "concave up" to being "concave down" or vice versa. They can be found by considering where the second derivative changes signs.
Therefore, we have to find the second derivative of the function $f\left( x \right)={{\left( x-5 \right)}^{55}}{{\left( x-6 \right)}^{66}}$.
We take logarithm for $y={{\left( x-5 \right)}^{55}}{{\left( x-6 \right)}^{66}}$. We get $\log y=55\log \left( x-5 \right)+66\log \left( x-6 \right)$.
We know that $\dfrac{d}{dx}\left( \log x \right)=\dfrac{1}{x}$. We use that for the differentiation where $\log y$.
For our given function, we can differentiate it to ${{f}^{'}}\left( x \right)=\dfrac{df}{dx}$.
On first differentiation, we get
$\begin{aligned} & \log y=55\log \left( x-5 \right)+66\log \left( x-6 \right) \\\ & \Rightarrow \dfrac{1}{y}\dfrac{dy}{dx}=\dfrac{55}{\left( x-5 \right)}+\dfrac{66}{\left( x-6 \right)} \\\ & \Rightarrow \dfrac{dy}{dx}=y\left[ \dfrac{55}{\left( x-5 \right)}+\dfrac{66}{\left( x-6 \right)} \right] \\\ \end{aligned}$
For the second derivative of the function, we can convert it to ${{f}^{''}}\left( x \right)=\dfrac{d\left( {{f}^{'}} \right)}{dx}$.
On second differentiation, we get
$\begin{aligned} & \dfrac{dy}{dx}=y\left[ \dfrac{55}{\left( x-5 \right)}+\dfrac{66}{\left( x-6 \right)} \right] \\\ & \Rightarrow \dfrac{{{d}^{2}}y}{d{{x}^{2}}}=\dfrac{dy}{dx}\left[ \dfrac{55}{\left( x-5 \right)}+\dfrac{66}{\left( x-6 \right)} \right]-y\left[ \dfrac{55}{{{\left( x-5 \right)}^{2}}}+\dfrac{66}{{{\left( x-6 \right)}^{2}}} \right] \\\ \end{aligned}$
We know that the solution for ${{f}^{'}}\left( x \right)=y\left[ \dfrac{55}{\left( x-5 \right)}+\dfrac{66}{\left( x-6 \right)} \right]$ is $x=5,6$.
We also show the changes as

domain of x	value of ${{f}^{'}}\left( x \right)$	characteristics
$x<5$	negative	concave down
$5 < x < 6$	positive	concave up
$x>6$	positive	concave up

Therefore, the function changes its concavity once. The correct option is B.
We try to explain this concept with the graph also.

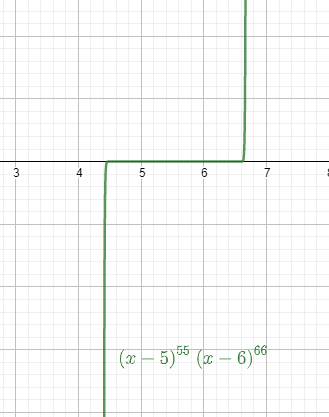
Note: We need to remember the concept of extremum and point of inflection is quite similar. The slopes decide the concavity and its change. We also need to remember that If a function is undefined at some value of x, there can be no inflection point.