Question

The point $\left( {4,1} \right)$ undergoes the following 3 transformations successively:
(i)Reflection about the line $y = x$
(ii)Translations through a distance of 2 units along the positive direction of $x$ axis.
(iii)Rotation through an angle $\dfrac{\pi }{4}$ about the origin in the anti-clockwise sense.
Then the final position of the point is given by:
A.$\left( {\dfrac{1}{{\sqrt 2 }},\dfrac{7}{{\sqrt 2 }}} \right)$
B.$\left( { - \sqrt 2 ,7\sqrt 2 } \right)$
C.$\left( { - \dfrac{1}{{\sqrt 2 }},\dfrac{7}{{\sqrt 2 }}} \right)$
D.$\left( {\sqrt 2 ,7\sqrt 2 } \right)$

Answer 1

We will find the image of the given point after reflection about the line $y = x$. We will then find the coordinates of the point after the translation of the image along the $x$ axis. We will use the formula for the rotation of a point about the origin to find the final position of the point.

Complete step-by-step answer:
If any point (say $\left( {a,b} \right)$) is reflected about the line $y = x$, then its image is the point $\left( {b,a} \right)$; that is the abscissa and the ordinate get interchanged.
So, the reflection of the point $\left( {4,1} \right)$ about the line $x = y$ will be the point $\left( {1,4} \right)$.

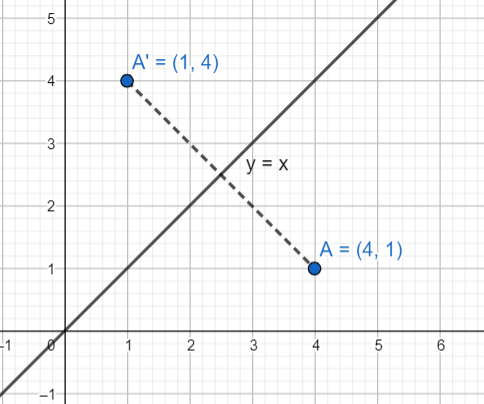
Now, the point is translated through a distance of 2 units along the positive direction of the$x$ axis.
So, the new point’s abscissa or the $x$ coordinate will be 2 units more than the older abscissa. We will find the new point:
$\Rightarrow \left( {1 + 2,4} \right) = \left( {3,4} \right)$

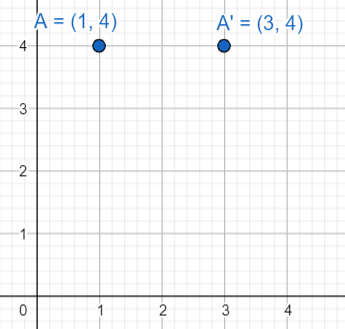
The new point will be $\left( {3,4} \right)$.
Now, the point is rotated through an angle $\dfrac{\pi }{4}$ about the origin in the anti-clockwise sense.

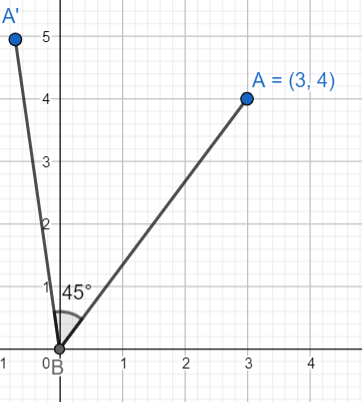
We will substitute $45^\circ$ for $\theta$, 3 for $a$ and 4 for $b$ in the formula for rotation of a point, $\left( {a\cos \theta - b\sin \theta ,a\cos \theta + b\sin \theta } \right)$. Therefore we get
$\left( {a\cos \theta - b\sin \theta ,a\cos \theta + b\sin \theta } \right) = \left( {3\cos 45^\circ - 4\sin 45^\circ ,3\cos 45^\circ + 4\sin 45^\circ } \right)$
Substituting the values of all trigonometric function, we get
$\begin{array}{l} \Rightarrow \left( {3\cos 45^\circ - 4\sin 45^\circ ,3\cos 45^\circ + 4\sin 45^\circ } \right) = \left( {\dfrac{3}{{\sqrt 2 }} - \dfrac{4}{{\sqrt 2 }},\dfrac{3}{{\sqrt 2 }} + \dfrac{4}{{\sqrt 2 }}} \right)\\\ \Rightarrow \left( {3\cos 45^\circ - 4\sin 45^\circ ,3\cos 45^\circ + 4\sin 45^\circ } \right) = \left( { - \dfrac{1}{{\sqrt 2 }},\dfrac{7}{{\sqrt 2 }}} \right)\end{array}$
$\therefore$ The final position of the point is $\left( { - \dfrac{1}{{\sqrt 2 }},\dfrac{7}{{\sqrt 2 }}} \right)$.
Option C is the correct option.

Note: If we get a case where the a point is rotated by an angle of $\theta$ about the origin in the clockwise direction, we will substitute $- \theta$ in the formula instead of $\theta$. We can derive this formula using vector calculus and the Pythagoras theorem.
When a point (say $\left( {a,b} \right)$) is rotated by an angle $\theta$ about the origin, then the coordinates of the new point are $\left( {a\cos \theta - b\sin \theta ,a\cos \theta + b\sin \theta } \right)$.