Question

The point A divides the join of P(-5,1) and Q(3,5) in the ratio k:1. The values of k for which the area of $\Delta ABC$where B(1,5), C(7,-2) is 2 square units is
A. $7,\dfrac{{31}}{9}$
B. $- 7,\dfrac{{31}}{9}$
C. $7,\dfrac{{ - 31}}{9}$
D. $- 7,\dfrac{{ - 31}}{9}$

Answer 1

According to the question we have to find the values of k when point A divides the join of P(-5,1) and Q(3,5) in the ratio k:1 and the area of $\Delta ABC$ where B(1,5), C(7,-2) is 2 square units. So, first of all we have to find the point A of $\Delta ABC$ with the help of the passage which is the join of P(-5,1) and Q(3,5) in the ratio k:1.
So, first of all we have to use the formula to find the point A of $\Delta ABC$ which is mentioned below.

Formula used: The coordinates of A in the figure given below when point A divides the line joining P and Q in the ratio m:n

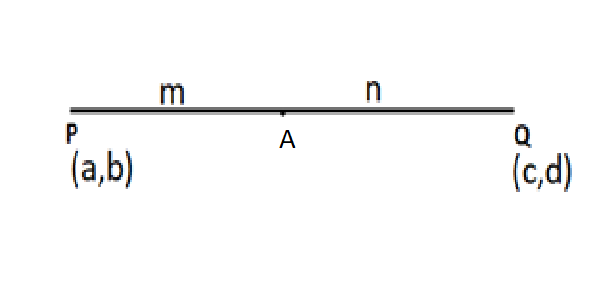
The coordinates of A = $\left( {\dfrac{{mc + na}}{{m + n}},\dfrac{{md + nb}}{{m + n}}} \right).......................(A)$
Now, we have to using the formula of triangle which is passing through the points $\left( {a,b} \right),\left( {c,d} \right)$and $\left( {e,f} \right)$that is mentioned below:
Formula used:
Area of triangle which is passing through the points $\left( {a,b} \right),\left( {c,d} \right)$and $\left( {e,f} \right)$ $= \dfrac{1}{2}\left| {a\left( {d - f} \right) + c\left( {f - b} \right) + e\left( {b - d} \right)} \right|...............................(B)$
According to the question, we have to make the formula (B) equals to 2 then find the desired values of k.

Complete answer:
Step 1: As given in the question that The point A divides the join of P(-5,1) and Q(3,5) in the ratio k:1
So, first of all we have to find the coordinates of A with the help of the formula (A) as mentioned in the solution hint.
The coordinates of A = $\left( {\dfrac{{3k + 1\left( { - 5} \right)}}{{k + 1}},\dfrac{{5k + 1}}{{k + 1}}} \right)$
$\Rightarrow$ $\left( {\dfrac{{3k - 5}}{{k + 1}},\dfrac{{5k + 1}}{{k + 1}}} \right)$
Step 2: As given in the question, the area of $\Delta ABC$where B(1,5), C(7,-2) is 2 square units.
Now, we have to using the formula (B) as mentioned in the solution hint for point A $\left( {\dfrac{{3k - 5}}{{k + 1}},\dfrac{{5k + 1}}{{k + 1}}} \right)$, point B(1,5) and point C(7,-2).
Area of triangle $\Delta ABC$ $= \dfrac{1}{2}\left| {\left( {\dfrac{{3k - 5}}{{k + 1}}} \right)\left( {5 - \left( { - 2} \right)} \right) + 1\left( { - 2 - \left( {\dfrac{{5k + 1}}{{k + 1}}} \right)} \right) + 7\left( {\dfrac{{5k + 1}}{{k + 1}} - 5} \right)} \right|$
$\Rightarrow 2$ $= \dfrac{1}{2}\left| {\left( {\dfrac{{3k - 5}}{{k + 1}}} \right)\left( {5 + 2} \right) + 1\left( { - 2 - \left( {\dfrac{{5k + 1}}{{k + 1}}} \right)} \right) + 7\left( {\dfrac{{5k + 1}}{{k + 1}} - 5} \right)} \right|$
Step 3: Now, we have to simplify the expression obtained in the solution step 2.
$\Rightarrow 2$ $= \dfrac{1}{2}\left| {\left( {\dfrac{{3k - 5}}{{k + 1}}} \right).7 + 1\left( {\dfrac{{ - 2(k + 1) - 5k - 1}}{{k + 1}}} \right) + 7\left( {\dfrac{{5k + 1 - 5(k + 1)}}{{k + 1}}} \right)} \right|$
$\Rightarrow 2$ $= \dfrac{1}{2}\left| {\left( {\dfrac{{21k - 35}}{{k + 1}}} \right) + \left( {\dfrac{{ - 2k - 2 - 5k - 1}}{{k + 1}}} \right) + 7\left( {\dfrac{{5k + 1 - 5k - 5}}{{k + 1}}} \right)} \right|$
$\Rightarrow 2$ $= \dfrac{1}{2}\left| {\left( {\dfrac{{21k - 35}}{{k + 1}}} \right) + \left( {\dfrac{{ - 2k - 2 - 5k - 1}}{{k + 1}}} \right) + \left( {\dfrac{{ - 28}}{{k + 1}}} \right)} \right|$
Step 4: now, we have to simplify the expression obtained in the solution step 3 by taking the L.C.M of fractions.
$\Rightarrow 2$ $= \dfrac{1}{2}\left| {\dfrac{{21k - 35 - 7k - 3 - 28}}{{k + 1}}} \right|$
$\Rightarrow 4$ $= \left| {\dfrac{{14k - 66}}{{k + 1}}} \right|....................(1)$
Step 5 : Now, we know that $\left| x \right| = x, - x$. So, we use this rule in the expression (1) of the solution step 4
$\Rightarrow 4$ $= \dfrac{{14k - 66}}{{k + 1}}$
$\Rightarrow 4(k + 1) = 14k - 66 \\\ \Rightarrow 4k + 4 = 14k - 66 \\\ \Rightarrow 4 + 66 = 14k - 4k \\\ \Rightarrow 70 = 10k \\\ \Rightarrow 7 = k \\\$
Now, taking the negative sign of $\left| {\dfrac{{14k - 66}}{{k + 1}}} \right|$which is$- \left( {\dfrac{{14k - 66}}{{k + 1}}} \right)$
$\Rightarrow 4$ $= - \left( {\dfrac{{14k - 66}}{{k + 1}}} \right)$
$\Rightarrow 4(k + 1) = - 14k + 66 \\\ \Rightarrow 4k + 4 = - 14k + 66 \\\ \Rightarrow 4k + 14k = 66 - 4 \\\ \Rightarrow 18k = 62k \\\ \Rightarrow k = \dfrac{{62}}{{18}} \\\ \Rightarrow k = \dfrac{{31}}{9} \\\$

Hence, we have to find the value of k that is $7,\dfrac{{31}}{9}$. Therefore option (A) is correct.

Note:
It is necessary that we have to determine the points which divide the given line with the help of the help of the section formula for internal division coordinates.
It is necessary that we have to use all the points which are given and obtained point A to determine the value of k with the help of the formula to find the area of the triangle.