Question

The point $(7,24)$ is on the terminal side of an angle in standard position, how do you determine the exact values of the six trigonometric functions of the angle?

Answer 1

Hint : In order to determine exact values of all six trigonometric function of the angle in the above question ,calculate $r = \sqrt {{x^2} + {y^2}}$ where x will be 7 and y will be 24.And then find all the trigonometric ratios considering Hypotenuse as r ,opposite as 24 and adjacent as 7.
Formula:

$$\sin \theta = \dfrac{{{\text{Opposite}}}}{{{\text{Hypotenuse}}}} \\\ \cos \theta = \dfrac{{Adjacent}}{{{\text{Hypotenuse}}}} \\\ \tan \theta = \dfrac{{{\text{Opposite}}}}{{Adjacent}} \\\ \cos ec\theta = \dfrac{{{\text{Hypotenuse}}}}{{{\text{Opposite}}}} \\\ sec\theta = \dfrac{{{\text{Hypotenuse}}}}{{Adjacent}} \\\ \cot \theta = \dfrac{{Adjacent}}{{{\text{Opposite}}}} \\\$$

Complete step-by-step answer :
Given a point P $(7,24)$ which is on the terminal side of an angle in standard position.
Let x be 7 and y be 24

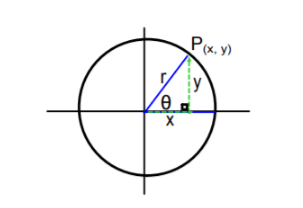
Calculating r using formula $r = \sqrt {{x^2} + {y^2}}$
$r = \sqrt {{{(7)}^2} + {{(24)}^2}} \\\ r = \sqrt {49 + 576} \\\ r = \sqrt {625} \\\ r = 25 \;$
Hence , value of r is $25$
Therefore Calculating all the trigonometric ratios as

$$\sin \theta = \dfrac{{{\text{Opposite}}}}{{{\text{Hypotenuse}}}} = \dfrac{y}{r} = \dfrac{{24}}{{25}} \\\ \cos \theta = \dfrac{{Adjacent}}{{{\text{Hypotenuse}}}} = \dfrac{x}{r} = \dfrac{7}{{25}} \\\ \tan \theta = \dfrac{{{\text{Opposite}}}}{{Adjacent}} = \dfrac{y}{x} = \dfrac{{24}}{7} \\\ \cos ec\theta = \dfrac{{{\text{Hypotenuse}}}}{{{\text{Opposite}}}} = \dfrac{r}{y} = \dfrac{{25}}{{24}} \\\ sec\theta = \dfrac{{{\text{Hypotenuse}}}}{{Adjacent}} = \dfrac{r}{x} = \dfrac{{25}}{7} \\\ \cot \theta = \dfrac{{Adjacent}}{{{\text{Opposite}}}} = \dfrac{x}{y} = \dfrac{7}{{24}} \;$$

Note : 1. Periodic Function= A function $f(x)$ is said to be a periodic function if there exists a real number T > 0 such that $f(x + T) = f(x)$ for all x.
If T is the smallest positive real number such that $f(x + T) = f(x)$ for all x, then T is called the fundamental period of $f(x)$ .
Since $\sin \,(2n\pi + \theta ) = \sin \theta$ for all values of $\theta$ and n $\in$ N.
2. Even Function – A function $f(x)$ is said to be an even function ,if $f( - x) = f(x)$ for all x in its domain.
Odd Function – A function $f(x)$ is said to be an even function ,if $f( - x) = - f(x)$ for all x in its domain.
We know that $\sin ( - \theta ) = - \sin \theta .\cos ( - \theta ) = \cos \theta \,and\,\tan ( - \theta ) = - \tan \theta$
Therefore, $\sin \theta$ and $\tan \theta$ and their reciprocals, $\cos ec\theta$ and $\cot \theta$ are odd functions whereas $\cos \theta$ and its reciprocal $\sec \theta$ are even functions.