Question

The point(4,-4) is on the terminal side of an angle in standard position, how do you determine the exact values of the six trigonometric functions of the angle?

Answer 1

In order to determine exact values of all six trigonometric function of the angle in the above question ,calculate $r = \sqrt {{x^2} + {y^2}}$ where x will be 4 and y will be -4.And then find all the trigonometric ratios considering Hypotenuse as r ,opposite as -4 and adjacent as 4.

Formula used:

$$\sin \theta = \dfrac{{{\text{Opposite}}}}{{{\text{Hypotenuse}}}} \\\ \cos \theta = \dfrac{{Adjacent}}{{{\text{Hypotenuse}}}} \\\ \tan \theta = \dfrac{{{\text{Opposite}}}}{{Adjacent}} \\\ \cos ec\theta = \dfrac{{{\text{Hypotenuse}}}}{{{\text{Opposite}}}} \\\ sec\theta = \dfrac{{{\text{Hypotenuse}}}}{{Adjacent}} \\\ \cot \theta = \dfrac{{Adjacent}}{{{\text{Opposite}}}} \\\$$

Complete step-by-step answer:
Given a point P(4,-4) which is on the terminal side of an angle in standard position.
Let x be 4 and y be -4

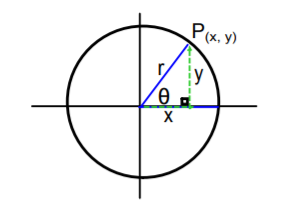
Calculating r using formula $r = \sqrt {{x^2} + {y^2}}$
$r = \sqrt {{{(4)}^2} + {{( - 4)}^2}} \\\ r = \sqrt {16 + 16} \\\ r = \sqrt {32} \\\ r = 4\sqrt 2 \\\$
Hence , value of r is $4\sqrt 2$
Therefore Calculating all the trigonometric ratios as

$$\sin \theta = \dfrac{{{\text{Opposite}}}}{{{\text{Hypotenuse}}}} = \dfrac{y}{r} = \dfrac{{ - 4}}{{4\sqrt 2 }} = \dfrac{{ - \sqrt 2 }}{2} \\\ \cos \theta = \dfrac{{Adjacent}}{{{\text{Hypotenuse}}}} = \dfrac{x}{r} = \dfrac{4}{{4\sqrt 2 }} = \dfrac{{\sqrt 2 }}{2} \\\ \tan \theta = \dfrac{{{\text{Opposite}}}}{{Adjacent}} = \dfrac{y}{x} = - 1 \\\ \cos ec\theta = \dfrac{{{\text{Hypotenuse}}}}{{{\text{Opposite}}}} = \dfrac{r}{y} = \dfrac{{ - 4\sqrt 2 }}{4} = - \sqrt 2 \\\ sec\theta = \dfrac{{{\text{Hypotenuse}}}}{{Adjacent}} = \dfrac{r}{x} = \dfrac{{4\sqrt 2 }}{4} = \sqrt 2 \\\ \cot \theta = \dfrac{{Adjacent}}{{{\text{Opposite}}}} = \dfrac{x}{y} = - 1 \\\$$

Note: 1. Periodic Function= A function $f(x)$ is said to be a periodic function if there exists a real number T > 0 such that $f(x + T) = f(x)$ for all x.
If T is the smallest positive real number such that $f(x + T) = f(x)$ for all x, then T is called the fundamental period of $f(x)$ .
Since $\sin \,(2n\pi + \theta ) = \sin \theta$ for all values of $\theta$ and n$\in$N.
2. Even Function – A function $f(x)$ is said to be an even function ,if $f( - x) = f(x)$for all x in its domain.
Odd Function – A function $f(x)$ is said to be an even function ,if $f( - x) = - f(x)$for all x in its domain.
We know that $\sin ( - \theta ) = - \sin \theta .\cos ( - \theta ) = \cos \theta \,and\,\tan ( - \theta ) = - \tan \theta$
Therefore,$\sin \theta$ and $\tan \theta$ and their reciprocals,$\cos ec\theta$ and $\cot \theta$ are odd functions whereas $\cos \theta$ and its reciprocal $\sec \theta$ are even functions.
3. Trigonometry is one of the significant branches throughout the entire existence of mathematics and this idea is given by a Greek mathematician Hipparchus.
4.One must be careful while taking values from the trigonometric table and cross-check at least once to avoid any error in the answer.