Question

The point $(-2m,m+1)$ is an interior point of the smaller region bounded by the circle ${{x}^{2}}+{{y}^{2}}=4$ and the parabola ${{y}^{2}}=4x$. Then $m$ belongs to the interval
(a). $-5-2\sqrt{6}<\,m<\,1$
(b). $0<\,m<\,4$
(c). $-1<\,m<\,\dfrac{3}{5}$
(d). $-1<\,m<\,-5+2\sqrt{6}$

Answer 1

Hint: First, find the points of intersection of the two curves, and then try to imagine which region will be smaller. Then use the property that if a point lies within the bowl shaped mouth of a parabola, then the value of ${{y}^{2}}-4ax<0$, for that point, and if it lies inside a circle, then the value we get on making it satisfy the equation of the circle will also be negative. Similarly, if it lies outside the bowl shaped mouth of the parabola, then the value of ${{y}^{2}}-4ax>0$, for that particular point.

Complete step-by-step answer:
Let’s call the circle having equation ${{x}^{2}}+{{y}^{2}}=4$ as S1 and the parabola having equation ${{y}^{2}}=4x$ as P1.
For S1, comparing it to the general equation of a circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$, we get :
$\begin{aligned} & 2gx=0x \\\ & \Rightarrow 2g=0 \\\ & \Rightarrow g=0 \\\ \end{aligned}$ and $\begin{aligned} & 2fy=0y \\\ & \Rightarrow 2f=0 \\\ & \Rightarrow f=0 \\\ \end{aligned}$
Thus, the centre of S1, $C1$= $(-g,-f)=(0,0)$ and its radius $r1=$ $\sqrt{{{g}^{2}}+{{f}^{2}}-c}=\sqrt{0+0+4}=2$.

For the parabola P1 now, comparing it to the general equation of a parabola ${{y}^{2}}=4ax$, we get :
$\begin{aligned} & 4ax=4x \\\ & \Rightarrow 4a=4 \\\ & \Rightarrow a=1 \\\ \end{aligned}$
Therefore, for P1, its focus $f1=$ $(a,0)=(1,0)$ and its vertex = $(0,0)$.
Now, let’s find out the points of intersection of S1 and P1.
We can do so simply by substituting for ${{y}^{2}}$ in S1 by using its value in terms of obtained from P1.
Doing so, we get :
$\begin{aligned} & {{x}^{2}}+{{y}^{2}}=4,{{y}^{2}}=4x \\\ & \Rightarrow {{x}^{2}}+4x=4 \\\ & \Rightarrow {{x}^{2}}+4x-4=0 \\\ & \Rightarrow x=\dfrac{-4\pm \sqrt{16+4\times 4}}{2} \\\ & \Rightarrow x=\dfrac{-4\pm 4\sqrt{2}}{2} \\\ & \Rightarrow x=-2\pm 2\sqrt{2} \\\ \end{aligned}$
We obtain two values from here for $x$. However, we can use only one value, since we need the value of $y$ to be real. All the equations we have for $y$ contain its square term, so if we’re using the equation of P1 to find $y$, we need that $4x>0$, since otherwise the value under root will become negative while finding $y$. Thus, we can accept only $x=2\sqrt{2}-2$ since this value will give us a real root, and $x=-2\sqrt{2}-2$ is rejected because it will give us a negative value under the root, and $y$ will be imaginary for this $x$.
Thus, working with $x=2\sqrt{2}-2$, we can substitute this into P1 to find $y$. Doing so, we get :
$\begin{aligned} & {{y}^{2}}=4x \\\ & \Rightarrow {{y}^{2}}=4(2\sqrt{2}-2) \\\ & \Rightarrow y=\pm \sqrt{8\sqrt{2}-8} \\\ & \Rightarrow y=\pm 2\sqrt{2\sqrt{2}-2} \\\ \end{aligned}$
Hence, we now have two values of $y$ for one value of $x$. This gives us two distinct points where S1 and P1 intersect. Since we took the positive value of $x$, this means that both the points have their $x$ coordinates $>0$ definitely. As for the $y$ coordinate, one value is positive, and one is negative. Hence, we know both these points are nothing but mirror images of each other with the $x$ axis acting as the mirror.
Try to imagine the figure on a graph now. S1 is a circle with its centre at (0,0) and its radius as 2. P1 is a parabola with its vertex at (0,0). The two intersection points lie in the 1st and 4th quadrants respectively. The circle is divided into half by the $y$ axis, but our intersection points lie in the 1st and 4th quadrants. So, the smaller region formed by the points of intersection will be enclosed between P1 and S1 in the 1st and 4th quadrant.

For any point $(x,y)$ in this smaller region, the conditions $\begin{aligned} & {{x}^{2}}+{{y}^{2}}-4<0 \\\ & {{y}^{2}}-4x<0 \\\ \end{aligned}$ will be true, since this point will lie inside the circle and also in the region that includes the axis of the parabola, for the parabola.

The point being talked about here = $(-2m,m+1)$
Substituting this point in both the conditions one by one, we get :
$\begin{aligned} & {{x}^{2}}+{{y}^{2}}-4<0 \\\ & \Rightarrow 4{{m}^{2}}+{{(m+1)}^{2}}-4<0 \\\ & \Rightarrow 4{{m}^{2}}+{{m}^{2}}+1+2m-4<0 \\\ & \Rightarrow 5{{m}^{2}}+2m-3<0 \\\ & \Rightarrow 5{{m}^{2}}+5m-3m-3<0 \\\ & \Rightarrow 5m(m+1)-3(m+1)<0 \\\ & \Rightarrow (5m-3)(m+1)<0 \\\ & \Rightarrow m\in (-1,\dfrac{3}{5}) \\\ \end{aligned}$ and $\begin{aligned} & {{y}^{2}}-4x<0 \\\ & \Rightarrow {{(m+1)}^{2}}-4(-2m)<0 \\\ & \Rightarrow {{m}^{2}}+1+2m+8m<0 \\\ & \Rightarrow {{m}^{2}}+10m+1<0 \\\ & \Rightarrow (m-\dfrac{-10+\sqrt{100-4}}{2})(m-\dfrac{-10-\sqrt{100-4}}{2})<0 \\\ & \Rightarrow (m-\dfrac{-10+\sqrt{96}}{2})(m-\dfrac{-10-\sqrt{96}}{2})<0 \\\ & \Rightarrow (m-\dfrac{-10+4\sqrt{6}}{2})(m-\dfrac{-10-4\sqrt{6}}{2})<0 \\\ & \Rightarrow (m-2\sqrt{6}+5)(m+2\sqrt{6}+5)<0 \\\ & \Rightarrow m\in (-5-2\sqrt{6},-5+2\sqrt{6}) \\\ \end{aligned}$
We now need to find the common intersection between these two conditions, to find the interval in which $m$ lies.
If we plot these intervals on a number line, we’ll find that the common interval will be : $m\in (-1,-5+2\sqrt{6})$
$\Rightarrow -1<\,m<\,-5+2\sqrt{6}$
Hence, the required interval is $-1<\,m<\,-5+2\sqrt{6}$.
Hence, option (d) is correct

Note: Here’s a diagram to illustrate the intersection points and the smaller region better :

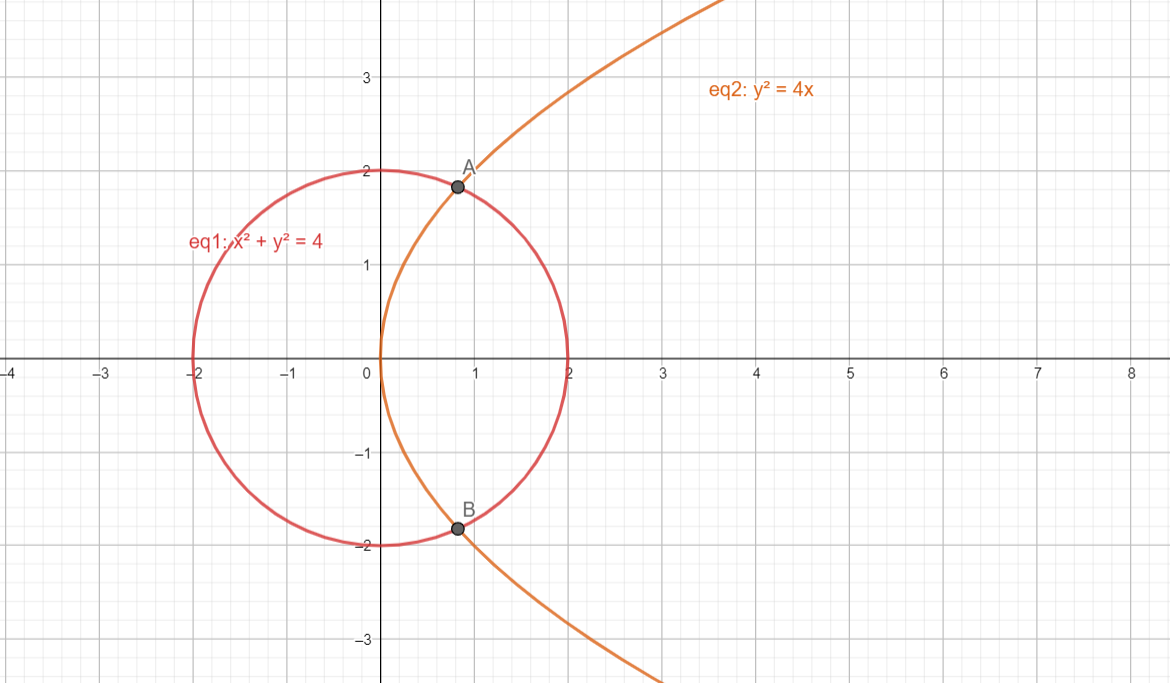
Here points $A$ and $B$ are the intersection points, as is visible, and the smaller region between the two does lie in the 1st and 4th quadrant.