Solveeit Logo
Login

Question

Question: The point (2,1) is translated parallel to the line L : x – y = 4 by \(2\sqrt 3 \)units. If the new p...

The point (2,1) is translated parallel to the line L : x – y = 4 by 232\sqrt 3 units. If the new point Q lies in the third quadrant, then the equation of the line passing through Q and perpendicular to L is
A.2x+2y=1−6 B.x+y=3−36 C.x+y=3−26 D.x+y=2−6  A.2x + 2y = 1 - \sqrt 6 \\\ B.x + y = 3 - 3\sqrt 6 \\\ C.x + y = 3 - 2\sqrt 6 \\\ D.x + y = 2 - \sqrt 6 \\\

Explanation

Solution

Draw the line x –y = 4 and with the help of slope and distance formula we can find the value of Q. With the point Q and it is given that the line is perpendicular to x –y =4, we can find the required equation using slope point formula.

Complete step-by-step answer:
Lets sketch the line x – y =4. Let the point (2 ,1) be P.
It is given that PQ is parallel to the x – y = 4.
Now let's draw the graph with the above details

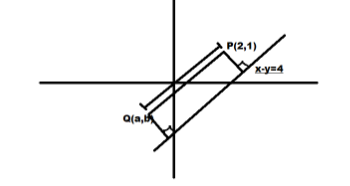
Step 2:
Let the new point be Q(a,b)
Now from the diagram , we can see that AQ is parallel to the given line.
The slope of the given line is 1
And since AQ is parallel , their slopes are equal
Therefore slope of AQ is 1
⇒y2−y1x2−x1=1 ⇒1−b2−a=1 ⇒1−b=2−a ⇒a−b=1 ⇒a=1+b  \Rightarrow \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} = 1 \\\ \Rightarrow \dfrac{{1 - b}}{{2 - a}} = 1 \\\ \Rightarrow 1 - b = 2 - a \\\ \Rightarrow a - b = 1 \\\ \Rightarrow a = 1 + b \\\
Let the above equation be equation (1)
Step 3:
It is also given that P(2 , 1) is at a distance of232\sqrt 3 units from Q
Distance between two points is given by
⇒(x1−x2)2+(y1−y2)2\Rightarrow \sqrt {{{({x_1} - {x_2})}^2} + {{({y_1} - {y_2})}^2}}
Here we already know that the distance between P and Q is 232\sqrt 3 units
Therefore ,
⇒(2−a)2+(1−b)2=23   \Rightarrow \sqrt {{{(2 - a)}^2} + {{(1 - b)}^2}} = 2\sqrt 3 \\\ \\\
Squaring on both sides we get,
⇒(2−a)2+(1−b)2=(23)2\Rightarrow {(2 - a)^2} + {(1 - b)^2} = {(2\sqrt 3 )^2}
Lets substitute equation (1) in the above equation
⇒(2−(1+b))2+(1−b)2=4∗3 ⇒(1−b)2+(1−b)2=12 ⇒2(1−b)2=12 ⇒(1−b)2=6 ⇒1−b=±6 ⇒b=1±6  \Rightarrow {(2 - (1 + b))^2} + {(1 - b)^2} = 4*3 \\\ \Rightarrow {(1 - b)^2} + {(1 - b)^2} = 12 \\\ \Rightarrow 2{(1 - b)^2} = 12 \\\ \Rightarrow {(1 - b)^2} = 6 \\\ \Rightarrow 1 - b = \pm \sqrt 6 \\\ \Rightarrow b = 1 \pm \sqrt 6 \\\
Substitute the value of b in equation (1)
⇒a=b+1 ⇒a=1±6+1=2±6  \Rightarrow a = b + 1 \\\ \Rightarrow a = 1 \pm \sqrt 6 + 1 = 2 \pm \sqrt 6 \\\
Step 4:
Here we have a=2±6a = 2 \pm \sqrt 6 and b=1±6b = 1 \pm \sqrt 6
Since the point Q lies in the third quadrant both the coordinates should be negative .
So a=2−6a = 2 - \sqrt 6 and b=1−6b = 1 - \sqrt 6
Step 5:
Now we need to find the equation of the line passing through Q and perpendicular to x – y =4
Slope of x –y=4 is 1
Since our required equation is perpendicular to x –y=4.
The slope of our required line is -1
By using slope point formula
(y−y1)=m(x−x1)(y - {y_1}) = m(x - {x_1})
We have
⇒(y−(1−6))=−1(x−(2−6)) ⇒(y−1+6)=−1(x−2+6) ⇒y−1+6=−x+2−6 ⇒x+y=2−6+1−6 ⇒x+y=3−26  \Rightarrow \left( {y - (1 - \sqrt 6 )} \right) = - 1\left( {x - (2 - \sqrt 6 )} \right) \\\ \Rightarrow \left( {y - 1 + \sqrt 6 } \right) = - 1\left( {x - 2 + \sqrt 6 } \right) \\\ \Rightarrow y - 1 + \sqrt 6 = - x + 2 - \sqrt 6 \\\ \Rightarrow x + y = 2 - \sqrt 6 + 1 - \sqrt 6 \\\ \Rightarrow x + y = 3 - 2\sqrt 6 \\\
Therefore the required equation is x+y=3−26x + y = 3 - 2\sqrt 6
The correct option is C.

Note: 1. Slope of parallel lines are equal.
2.Product of the slope of perpendicular lines is -1.
3.In a graph, there are four quadrants based on the sign of x and y coordinate. In the first quadrant both x and y are positive and in the second quadrant x is negative and y is positive , in the third quadrant both x and y are negative and in the fourth quadrant y is negative and x is positive.