Question

The plots of log V vs. log T at constant P for 1 mole of an ideal gas gives intercept equal to:
A.$\log \dfrac{P}{R}$
B.$- \dfrac{P}{R}$
C.$- \dfrac{R}{P}$
D.$\log \dfrac{R}{P}$

Answer 1

We can use the ideal gas equation to solve this problem. The ideal gas equation can be rearranged to obtain the graph. We know that the log V vs log T graph will yield us a straight line. By using the straight-line equation, we can say that y=mx+c and thus the value of c will give us the value of the intercept.

Complete answer:
According to the ideal gas equation we can say that
$\Rightarrow PV = nRT$
This means that the pressure, volume, Temperature and the universal gas constant R can be related by this formula.
According to the question, we are given 1 mole of the gas. This means that the value of n=1.
Thus the equation becomes:
$\Rightarrow PV = RT$
Applying logarithm on both the sides we get,
$\Rightarrow \log P + \log V = \log R + \log T$
$\Rightarrow \log V = \log R + \log T - \log P$
By simplifying the logarithm we will obtain:
$\Rightarrow \log V = \log \dfrac{R}{P} + \log T$
This is of the form y=mx+c
Here log V is in the y-axis and log T is in the x-axis. Thus we can say that the value of c will be $\log \dfrac{R}{P}$ .
The graph of the equation will be given by:

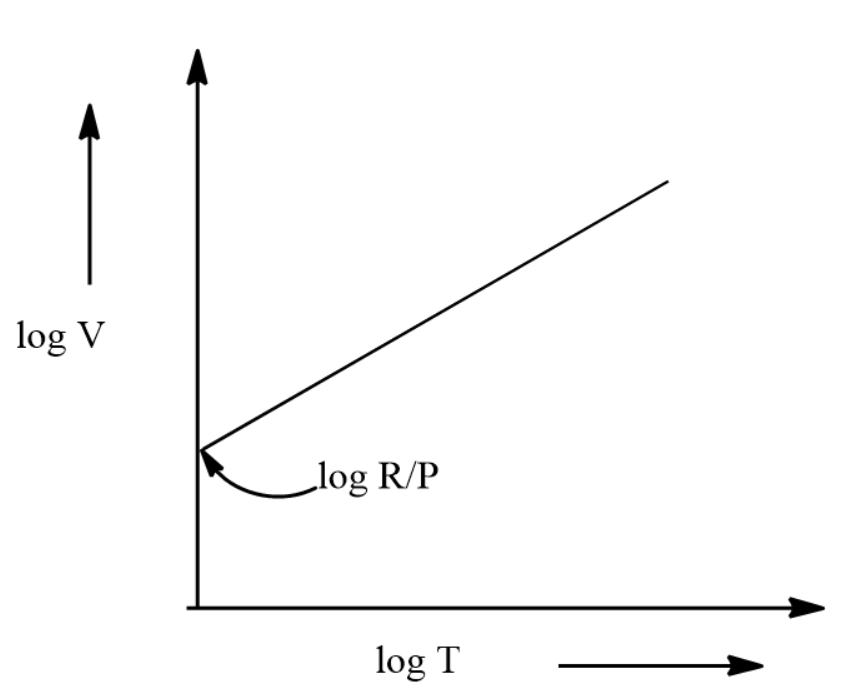
Hence the correct answer is option D.

Note:
While doing the simplification of the log terms we are taking the log P term to the right-hand side instead of log V because the value of P is a constant and thus the value of intercept obtained can be a constant. It is mentioned in the question that the experiment is done under constant pressure. Thus we need the intercept term to be a constant value and hence use P in it.