Question

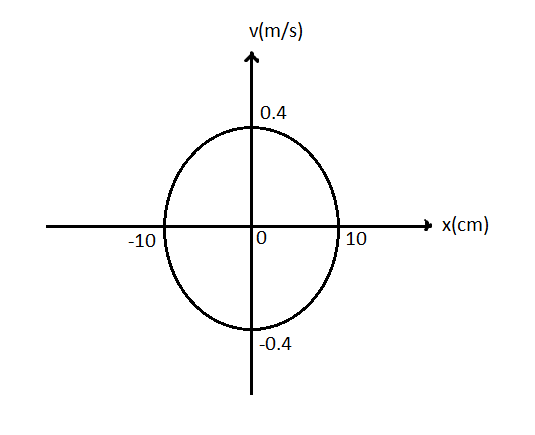
The plot velocity (v) versus displacement (x) of a particle executing simple harmonic motion in the figure. The time period of oscillation of particle is:

A) $\dfrac{\pi }{2}s$
B) $\pi s$
C) $2\pi s$
D) $3\pi s$

Answer 1

A simple harmonic motion is an example of periodic motion. In simple harmonic motion, a particle is accelerated towards a fixed point (in this case, O) and the acceleration of the particle will be proportional to the magnitude of the displacement of the particle. We have to use the velocity and amplitude of the particle, which is given in the diagram to find the angular velocity. The time period can be calculated from that.

Formula used:
${v_{\max }} = A\omega$ (Where ${v_{\max }}$stands for the maximum velocity of the particle, $A$is the amplitude of the particle, $\omega$is the angular velocity of the particle)
$T = \dfrac{{2\pi }}{\omega }$ (Where $T$is the time period of oscillation, $2\pi$is a constant)

Complete step by step solution:
In the velocity-displacement graph given in the question, the $x$axis gives the value of displacement and the $y$axis gives the value of velocity.
For a simple harmonic oscillator, the maximum velocity is given by
${v_{\max }} = A\omega$
From this equation, the angular velocity can be deduced as
$\omega = \dfrac{{{v_{\max }}}}{A}$………………………..($1$)
From the graph,
The maximum displacement of the particle i.e. the amplitude,$A = 10cm$ $= 10 \times {10^{ - 2}}m$ $(\because 1cm = {10^{ - 2}}m)$
The maximum velocity of the particle, ${v_{\max }} = 0.4m/s$
Substituting the values $A$ and $\omega$ in equation ($1$)
$\omega = \dfrac{{0.4}}{{10 \times {{10}^{ - 2}}}} = 4{s^{ - 1}}$
The time period of a simple harmonic oscillator is given by,
$T = \dfrac{{2\pi }}{\omega }$
Substituting the value of $\omega$in the equation,
$T$ = $\dfrac{{2\pi }}{4} = \dfrac{\pi }{2}s$

The answer is Option (A), $\dfrac{\pi }{2}s.$

Note: The typical example of simple harmonic motion is the oscillation of a mass suspended at the end of a spring. The fixed point from which the particle starts moving is called the equilibrium position. The restoring force directed towards the equilibrium position will obey Hooke’s law. All simple harmonic motions are periodic but all periodic motions are not simple harmonic.