Question
Question: The plot represents the flow of current through a wire at three different times. The ratio of charge...
The plot represents the flow of current through a wire at three different times. The ratio of charge flowing through the wire at three different times is
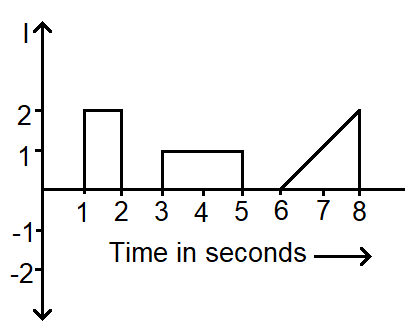
(A) 2:1:2
(B) 1:3:3
(C) 1:1:1
(D) 2:3:4
Solution
Hint In a current v/s time plot, the charge is given by the area under the curve. So we can calculate the area under the curve at three different times and then by finding their ratio, we can find the charge flowing through the wire at three different times.
Formula Used: In this solution we will be using the following formula,
⇒I=dtdq
where I is the current in the wire,
q is the charge flowing and t is the time.
Complete step by step answer
In the question we are given the plot of the current flowing through a wire. Now the current in a wire and the charge flowing is related by the formula,
⇒I=dtdq
Now taking the dt from the denominator of the RHS to the LHS to get,
⇒dq=Idt
Therefore, in a plot of current and time, the charge will be given by the area under the curve. So let us name the 3 curves as 1, 2 and 3.
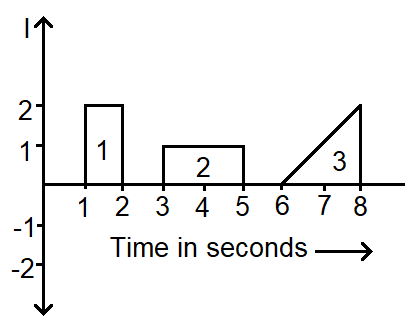
Now for the first plot, we can see that it is a rectangle.
According to the figure, the sides of the rectangle are 2A along the Y-axis and 1salong the X-axis.
So we have the area as,
⇒A1=2×1=2C
Now for the second plot, we can see that it is a rectangle.
According to the figure, the sides of the rectangle are 1A along the Y-axis and 2salong the X-axis.
So we have the area as,
⇒A2=1×2=2C
Now for the third plot, we can see that it is a triangle.
According to the figure, the height of the triangle is 2A along the Y-axis and the base is 2s along the X-axis.
So we have the area as,
⇒A2=21×2×2=2C
Therefore the ratio of the charges will be the ratio of the areas under the plot,
⇒A1:A2:A3=2:2:2
So the ratio is 1:1:1
Hence the correct answer is option C.
Note
When there are charges moving through a wire, then a current is generated in the wire. Hence the rate of flow of charge through a wire per unit time is called the current in the wire. The unit of current in the wire is coulomb and it is denoted by the letter C.
