Question

The plates of a parallel plate capacitor are charged upto $100V$ . A $2mm$ thick insulator shunt is inserted between the plates. Then to maintain the same potential difference, the distance between the capacitor plates is increased by $1.6mm$ . The dielectric constant of the insulator is
A. $5$
B. $8$
C. $4$
D. $6$

Answer 1

Assume the initial distance between the parallel plate capacitor be $d = 2mm$. A thick insulator is inserted between the plates. The charge and the potential difference are maintained the same. We know that charge $q$ on a capacitor is given as $q = CV$ where $C$ is the capacitance of the capacitor and $V$ is the potential difference. As $q,V$ remains same thus, the capacitance of the capacitor after insertion of the insulator must be equal. Using this, we can find the value of the dielectric constant of the insulator.

Complete step by step answer:
Let us write down the given quantities:
The potential difference is given as, $V = 100V$
The thickness of the insulator, ${d_0} = 2mm$
The distance is increased by, ${d_{air}} = 1.6mm$ as the medium will be air.
The charge on the capacitor remains same, let that charge be: $q$
Consider the following diagram:

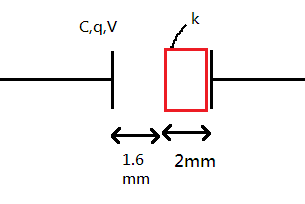
From the figure, we can clearly see that the total distance between the parallel plate is now $1.6mm + 2mm = 3.6mm$ .
We can consider that there are two insulators between the parallel plates of capacitors connected in series; air and the insulator having dielectric constant $K$ . For air, the value of dielectric constant is ${K_{air}} = 1$ . For series combination the effective capacitance ${C_{effective}}$ will be given as:
$\dfrac{1}{{{C_{effective}}}} = \dfrac{1}{{\dfrac{{K{\varepsilon _o}A}}{{{d_0}}}}} + \dfrac{1}{{\dfrac{{{K_{air}}{\varepsilon _o}A}}{{{d_{air}}}}}}$
Here, $K$ is the dielectric constant of the insulator,
$A$ is the area of the plates
${\varepsilon _o}$ is the relative permittivity of space having value ${\varepsilon _o} = 8.854 \times {10^{ - 12}}F{m^{ - 1}}$
${C_{effective}} = \dfrac{{\dfrac{{K{\varepsilon _o}A}}{{{d_0}}} \times \dfrac{{{\varepsilon _o}A}}{{{d_{air}}}}}}{{\dfrac{{K{\varepsilon _o}A}}{{{d_0}}} + \dfrac{{{\varepsilon _o}A}}{{{d_{air}}}}}}$ (as ${K_{air}} = 1$ )
$\Rightarrow {C_{effective}} = \left( {\dfrac{{\dfrac{K}{{{d_0}}} \times \dfrac{{{\varepsilon _o}A}}{{{d_{air}}}}}}{{\dfrac{K}{{{d_0}}} + \dfrac{1}{{{d_{air}}}}}}} \right)$ (taking ${\varepsilon _o}A$ common from numerator and denominator)
It is given that ${d_{air}} = 1.6mm$ and ${d_0} = 2mm$ , substituting these values we get:
$\Rightarrow {C_{effective}} = \left( {\dfrac{{\dfrac{K}{2} \times \dfrac{{{\varepsilon _o}A}}{{1.6}}}}{{\dfrac{K}{2} + \dfrac{1}{{1.6}}}}} \right)$
$\Rightarrow {C_{effective}} = \left( {\dfrac{{{\rm K}{\varepsilon _o}A}}{{1.6K + 2}}} \right)$ --equation $1$
The initial capacitance ${C_{initial}}$ when the insulator was not inserted and the distance between plates $d = 2mm$ , and the medium between plates was air, will be:
${C_{initial}} = \dfrac{{{K_{air}}{\varepsilon _o}A}}{d}$
But ${K_{air}} = 1$
$\Rightarrow {C_{initial}} = \dfrac{{{\varepsilon _o}A}}{2}$ -- equation $2$
Charge on capacitor is given as:
$q = CV$
$\Rightarrow \dfrac{q}{V} = C$
But we are given that charge and potential remain the same. Therefore, the capacitance must be equal:
${C_{initial}} = {C_{effective}}$
From equation $1$ and equation $2$ , we have
$\Rightarrow \dfrac{{{\varepsilon _o}A}}{2} = \left( {\dfrac{{{\rm K}{\varepsilon _o}A}}{{1.6K + 2}}} \right)$
$\Rightarrow \dfrac{1}{2} = \left( {\dfrac{{\rm K}}{{1.6K + 2}}} \right)$ taking ${\varepsilon _o}A$ common
$\Rightarrow 1.6K + 2 = 2k$
$\Rightarrow 2k - 1.6K = 2$
$\Rightarrow 0.4K = 2$
$\Rightarrow K = 5$
Therefore, the value of dielectric constant is $K = 5$

So, the correct answer is “Option A”.

Note:
The effective capacitance for parallel combination is the given as: ${C_{effective}} = \dfrac{{{C_1}{C_2}}}{{{C_1} + {C_2}}}$ .
Here, ${C_1},{C_2}$ is the individual capacitances. The dielectric constant for air is ${K_{air}} = 1$ .
If the medium between plates of capacitor is not mentioned it is taken as air and not vacuum.