Question
Question: The plane \(XOZ\) divides the join of \(\left( 1,-1,5 \right)\) and \(\left( 2,3,4 \right)\) in the ...
The plane XOZ divides the join of (1,−1,5) and (2,3,4) in the ratio λ:1, then λ is
A. -3
B. 41
C. 3
D. 31
Solution
Hint: We know that in XOZ plane, we have the y coordinates as equal to 0. We will find the value of λ using this concept as y=o divides the join of (1,−1,5) and (2,3,4) in the ratio λ:1, so we get, λ+13λ−1=0.
Complete step-by-step solution -
It has been given in the question that the plane XOZ divides the join of (1,−1,5) and (2,3,4) in the ratio λ:1 and we have to find the value of λ. We know that in the XZ plane, the coordinates of y axis is 0, or we get, y=o. We also know that XOZ divides the join of (1,−1,5) and (2,3,4) in the ratio λ:1.
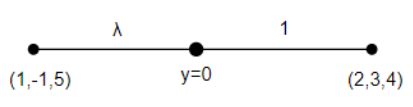
Now we will find the coordinates of X and Z. We know that for any two points, (x1,x2) and (y1,y2), when they are divided by any point in the ratio of m:n, then they can be written as, (m1n)=m+nx2(m)+x1(n),m+ny2(m)+y1(n) .
But here we have to find (X,Z) because the point, y=o. So, we can write it as,
λ+13(λ)+(−1)(1)=0⇒λ+13λ−1=0⇒3λ−1=0⇒3λ=1⇒λ=31
Thus, the value of λ is 31 and the plane XOZ divides the point in the ratio of 31:1.
Therefore, the correct answer to the given question is option D, 31.
Note: In this type of questions, the students usually find the line using the two given points, (x1,x2,x3) and (y1,y2,y3), then they use the ratio λ:1 to divide and find the value of λ, but that is quite a long method. On the other hand, if we apply only a single concept, that is, in a plane (X,Z), the coordinates of y=o, we can directly find the value of λ as we have done in the question.
